已知点 C 在线段 AB 上，则下列条件中，不能确定点 C 是线段 AB 中点的是（　　）

A ． AC ＝ BC B ． AB ＝ 2AC C ． AC+BC ＝ AB D ．

如图， ∠ AOB=60° ，点 P 是 ∠ AOB 内的定点且 OP= ，若点 M、N 分别是射线 OA、OB 上异于点 O 的动点，则 △ PMN 周长的最小值是（　　）

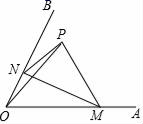
A ． B ． C ． 6 D ． 3

如图，已知直线上顺次三个点 A 、 B 、 C ，已知 AB ＝ 10cm ， BC ＝ 4cm ． D 是 AC 的中点， M 是 AB 的中点，那么 MD ＝（　　） cm

A ． 4 B ． 3 C ． 2 D ． 1

如图，点 是线段 上一点， 为 的中点，且 ， . 若点 在直线 上，且 ，则 的长为（ ）

A ． B ． C ． 或 D ． 或

两根木条，一根长 20cm ，另一根长 24cm ，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为 (　　)

A ． 2cm B ． 4cm C ． 2cm 或 22cm D ． 4cm 或 44cm

如图，在等边 △ ABC 中， BF 是 AC 边上的中线，点 D 在 BF 上，连接 AD ，在 AD 的右侧作等边 △ ADE ，连接 EF ，当 △ AEF 周长最小时， ∠ CFE 的大小是 (　　)

A ． 30° B ． 45° C ． 60° D ． 90°

如图，点 C 是线段 AB 上的点，点 D 是线段 BC 的中点， AB=10，AC=6 ，则线段 AD 的长是（　　）

A ． 6 B ． 2 C ． 8 D ． 4

如图， C，D是线段AB上的两个点，CD＝3 cm，M是AC的中点，N是DB的中点，AB＝7.8 cm，那么线段MN的长等于(     )

A ． 5.4 cm B ． 5.6 cm C ． 5.8 cm D ． 6 cm

如图，已知直线 AB：y= x+ 分别交 x 轴、 y 轴于点 B、A 两点 ,C（3，0），D、E 分别为线段 AO 和线段 AC 上一动点， BE 交 y 轴于点 H, 且 AD＝CE ，当 BD＋BE 的值最小时，则 H 点的坐标为（ ）

A ． （ 0，4） B ． （ 0，5） C ． （ 0， ） D ． （ 0， ）

如图，小红想用一条彩带缠绕易拉罐，正好从 A 点绕到正上方 B 点共四圈，已知易拉罐底面周长是 12 cm ，高是 20 cm ，那么所需彩带最短的是 ( )

A ． 13 cm B ． 4 cm C ． 4 cm D ． 52 cm