古筝是中国独特的民族乐器之一,为了保持音准,弹奏者常使用调音器对每根琴弦进行调音.如图,这是某古筝调音器的界面,指针指向 40 表示音调偏高,需放松琴弦.下列指针指向的数字中表示需拧紧琴弦,且最接近标准音(指针指在 0 处为标准音)的是( )

A . B .
C . 10 D . 20
B
【分析】根据正负数以及绝对值表示的含义解题即可.
本题主要考查了正数和负数,理解正负数表示的含义是解题的关键.
【详解】解:由题意可知,指针指向负数表示音调偏低,需拧紧琴弦,
又 指针越接近 0 就越接近标准音,
,
,
更接近 0
故选: B .
小圆身高 ,以小圆的身高为标准,小圆爸爸的身高为
,记作
,那么小圆妈妈的身高为
应记为( )
A . B .
C .
D .
C
【分析】本题考查了正数和负数,相反意义的量用正数和负数表示.根据正数和负数表示相反意义的量,高于标准记为正,低于标准的用负数表示,可得答案.
【详解】解:小圆身高 ,以小圆的身高为标准,小圆爸爸的身高为
,记作
,那么小圆妈妈的身高为
应记为
,
故选: C .
如果 吨表示运出仓库的大米吨数,那么运入 5 吨大米表示为( )
A . 吨 B .
吨 C .
吨 D .
吨
B
【分析】本题主要考查正负数的意义,根据正负数的意义可进行求解.熟练掌握正负数的意义是解题的关键.用正数和负数表示具有相反意义的量,其中一个量用正数表示,则与之相反的量用负数表示.
【详解】 ∵ 吨表示运出仓库的大米吨数,
∴ 运入 5 吨大米表示为 吨.
故选: B .
《九章算术》中注有 “ 今两算得失相反,要令正负以名之 ” ,意思是:今有两数若其意义相反,则分别叫做正数与负数.若收入 80 元记作 元,则
元表示( )
A .收入 50 元 B .收入 30 元 C .支出 50 元 D .支出 30 元
D
【分析】本题考查了正数和负数.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【详解】解:根据题意,若收入 80 元记作 元,则
元表示支出 30 元.
故选: D .
如果把一个物体向右移动 1 米记作移动 米,那么这个物体向左移动 1 米记作移动( )
A . 米 B .
米 C .
米 D . 0 米
B
【分析】本题考查了正数和负数,根据在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示解答即可.
【详解】解:如果把一个物体向右移动 1 米记作移动 米,那么这个物体向左移动 1 米记作移动
米,
故选: B .
如图是小才国庆期间的微信支付情况,微信账单中的 表示的意思是( )
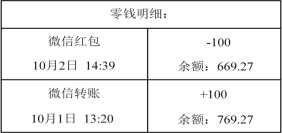
A .发出 元红包 B .余额
元
C .收入 元 D .抢到
元红包
A
【分析】本题考查用负数表示相反意义的量,根据相反意义的量可以用正负数来表示,正数表示收到,则负数表示发出,据此解答即可.
【详解】解:由题意可知, 表示的意思是发出 100 元红包.
故选: A .
如果零上 记作
,那么零下
可记为( )
A . B .
C .
D .
B
【分析】此题考查的是正负数的意义.根据正负数的意义:表示具有相反意义的量,即可得出结论.
【详解】解: ∵ 零上 记作
,
∴ 零下 可记为
.
故选: B
若盈利 2 万元记作 万元,则
万元表示( )
A .亏损 万元 B .盈利 4 万元 C .亏损 4 万元 D .不盈利也不亏损
C
【分析】本题考查了正负数的意义.熟练掌握正负数的意义是解题的关键.
由盈利记作 ,亏损记作
,进行作答即可.
【详解】解:由题意知, 万元表示亏损 4 万元,
故选: C .
《九章算术》中有 “ 今两算得失相反,要令正负以名之 ” ,意思是:今有两数,若其意义相反,则分别叫做正数和负数.如果盈利 70 元记作 元,那么亏 50 元记作( )
A . 元 B .
元 C .
元 D .
元
A
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【详解】解:根据题意,若盈利 70 元记作 元,那么亏 50 元记作
元.
故选: A .
【点睛】本题考查了正数和负数,解题关键是理解 “ 正 ” 和 “ 负 ” 的相对性,确定一对具有相反意义的量.
中国是最早采用正负数表示相反意义的量的国家,如果将 “ 收入 元 ” 记作 “
元 ” ,那么 “ 支出 40 元 ” 记作( )
A . 元 B .
元 C .
元 D .
元
B
【分析】本题考查了正负数的意义, “ 收入 元 ” 记作 “
元 ” ,那么 “ 支出 40 元 ” 即为 “
元 ” ,即可作答.
【详解】解:依题意,
因为 “ 收入 元 ” 记作 “
元 ” ,
所以 “ 支出 40 元 ” 记作 “ 元 ” ,
故选: B .
一个物体作上下方向的运动,规定向上运动 记作
,那么向下运动
记作( )
A . B .
C .
D .
B
【分析】本题考查正负数的意义和表示;根据正负数的意义,结合题意求解即可,理解正负数意义是解题的关键.
【详解】解: ∵ 规定向上运动 记作
,
∴ 向下运动 记作
,
故选: B .
绿色植物是氧气的生产者和二氧化碳的消耗者,把生产的氧气用正数表示,消耗的二氧化碳用负数表示,一公顷阔叶林一天生产 千克氧气可记作
千克,那么一天消耗
千克二氧化碳应记作 .
千克
【分析】本题考查了正负数的意义,根据生产与消耗是一对相反意义的量,进行作答即可.
【详解】解:依题意,因为一公顷阔叶林一天生产 千克氧气可记作
千克,
所以那么一天消耗 千克二氧化碳应记作
千克,
故答案为: 千克
如果 表示 “ 向北航行
” 那么 “ 向南航行
” 可以表示为
.
【分析】本题考查了正负数的意义 . 熟练掌握正负数的意义是解题的关键 .
根据正负数的意义进行作答即可 .
【详解】 解:由题意知,向南航行 表示为
,
故答案为: .
若气温为零上 ,记作
,则气温为零下
,记作 ℃ .
【分析】本题考查了正数和负数的意义,根据 “ 正数和负数表示具有相反意义的量 ” ,即可解答.
【详解】解: ∵ 零上 ,记作
,
∴ 零下 ,记作
,
故答案为: .
若零上 记作
,则零下
记作 .
【分析】本题考查了正数和负数的知识.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示,据此求解即可.
【详解】解:若零上 记作
,则零下
记作
,
故答案为: .
如果气温上升 记作
,那么气温下降
记作
.
【分析】此题考查用正负数来表示具有意义相反的两种量:零上温度记为正,则零下温度就记为负,直接得出结论即可.
【详解】解:如果气温上升 记作
,那么气温下降
记作
;
故答案为: .
如果电梯上升 5 层记为 ,那么电梯下降 2 层应记为
【分析】此题主要考查了正数和负数,直接利用电梯上升 5 层记为 ,则电梯下降记为负数,进而得出答案.
【详解】解: ∵ 电梯上升 5 层记为 ,
∴ 电梯下降 2 层应记为: .
故答案为: .
某蓄水池的标准水位记为 0m ,如果用正数表示水面高于标准水位的高度,那么水面低于标准水位 可表示为 .
【分析】此题主要考查了正负数的意义,首先审清题意,明确 “ 正 ” 和 “ 负 ” 所表示的意义;再根据题意作答.
【详解】根据题意,水面低于标准水位 可表示为
.
故答案为: .
中国是最早采用正负数来表示相反意义的量的国家,战国时期李所著的《法经》中已使用负数.在比赛中,加 20 分记作 分,扣 10 分记作 .
分
【分析】本题考查正数和负数,根据正数和负数是一组具有相反意义的量,据此即可求得答案.
【详解】解:在比赛中,加 20 分记作 分,扣 10 分记作
分,
故答案为: 分.
若收入 8 元记作 元,那么支出 10 元记作 元.
【分析】本题考查了正负数在实际生活中的应用,解题的关键是理解 “ 正 ” 和 “ 负 ” 的相对性,确定一对具有相反意义的量.本题收入记住 “ + ” ,则支出记作 “ ” ,据此即可求解.
【详解】解:如果收入 元记作
元,那么支出
元记作:
元.
故答案为: .
查看答案
单次付费有效 3.99 元
用于查看答案,单次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP无限次 49.99元