在 1 ,- 2 , 0 , 这四个数中,最大的数是( )
A . 1 B .- 2 C . 0 D .
D
【分析】根据实数的大小比较法则 “ 正数> 0 >负数;两个负数比大小,绝对值大的反而小 ” 进行比较分析.
【详解】解: ∵ ,
∴ 最大的数是
故选: D .
【点睛】本题考查实数的大小比较,理解 “ 正数> 0 >负数;两个负数比大小,绝对值大的反而小 ” 是解题关键.
如图是一个立体图形的三视图,该立体图形是( )
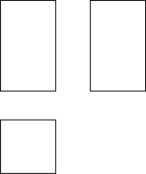
A .长方体 B .正方体 C .三棱柱 D .圆柱
A
【分析】根据题意可得这个几何体的三视图为长方形和正方形,即可求解.
【详解】解:根据题意得:该几何体的三视图为长方形和正方形,
∴ 该几何体是长方体.
故选: A
【点睛】本题考查由三视图确定几何体的名称,熟记常见几何体的三视图的特征是解题的关键.
下列说法正确的是( )
A .为了解我国中小学生的睡眠情况,应采取全面调查的方式
B .一组数据 1 , 2 , 5 , 5 , 5 , 3 , 3 的众数和平均数都是 3
C .若甲、乙两组数的方差分别是 0.01 , 0.1 ,则甲组数据比乙组数据更稳定
D .抛掷一枚硬币 200 次,一定有 100 次 “ 正面向上 ”
C
【分析】可根据调查的选择、平均数和众数的求法、方差及随机事件的意义,逐个判断得结论.
【详解】解:因为我国中小学生人数众多,其睡眠情况也不需要特别精确,
所以对我国中小学生的睡眠情况的调查,宜采用抽样调查,故选项 A 不正确;
因为 B 中数据据 1 , 2 , 5 , 5 , 5 , 3 , 3 ,重复出现次数最多的是 5 ,平均数为 ,故该组数据的众数与平均数都不是 3 ,,
所以选项 B 说法不正确;
因为 0.01 < 0.1 ,方差越小,波动越小,数据越稳定,
所以甲组数据比乙组数据稳定,故选项 C 说法正确;
因为抛掷硬币属于随机事件,抛掷一枚硬币 200 次,不一定有 100 次 “ 正面朝上 ”
故选项 D 说法不正确.
故选: C .
【点睛】本题的关键在于掌握调查的选择、平均数和众数的求法、方差及随机事件的意义.
如图, ,直线 EF 分别交 AB 、 CD 于 E 、 F 两点, ∠ BEF 的平分线交 CD 于点 G ,若 ∠ EFG =52° ,则 ∠ EGF 等于( )
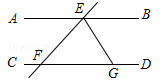
A . 26° B . 64° C . 52° D . 128°
B
【分析】根据平行线的性质及角平分线的定义解答即可.
【详解】解: ∵ ,
∴∠ BEF +∠ EFG =180° ,
∴∠ BEF =180° ﹣ 52°=128° ;
∵ EG 平分 ∠ BEF ,
∴∠ BEG =64° ;
∴∠ EGF =∠ BEG =64° (内错角相等).
故选: B .
【点睛】本题考查了平行线的性质,角平分线的定义,解答本题用到的知识点为:两直线平行,内错角相等;角平分线分得相等的两角.
下列各式计算正确的是( )
A . B .
C .
D .
C
【分析】由合并同类二次根式判断 A , B ,由二次根式的乘除法判断 C , D .
【详解】解: A 、 原计算错误,该选项不符合题意;
B 、 原计算错误,该选项不符合题意;
C 、 正确,该选项符合题意;
D 、 原计算错误,该选项不符合题意;
故选: C .
【点睛】本题考查合并同类二次根式,二次根式的乘法,二次根式的乘方运算,掌握以上知识是解题关键.
本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户呵呵呵分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。