2021-2022学年初中八年级第十七单元数学练习题含解析
初中
整体难度：中等
2022-06-14
题号
一
二
三
四
五
评分
一、选择题 (共25题)
添加该题型下试题
1.
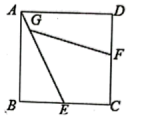
如图，正方形 ABCD 的边长为 6 ，点 E ， F 分别是边 BC 和 CD 的中点，连接 AE ，在 AE 上取点 G ，连接 GF ，若 ，则 GF 的长为（ ）
A ． B ．
C ．
D ．
难度：
知识点：勾股定理
使用次数：268
【答案】
C
【解析】
【分析】
根据已知条件，连接 AF 、 EF ，过点 F 作 FM ⊥ AE ，垂足为 M ，构造关于 GF 的直角三角形，解直角三角形即可求出 GF 的长．
【详解】
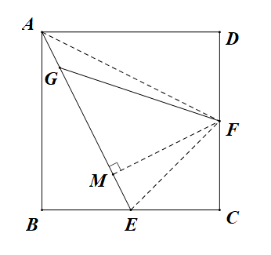
解：如图，连接 AF 、 EF ，过点 F 作 FM ⊥ AE ，垂足为 M ，
∵ 正方形 ABCD 边长为 6 ，点 E 、 F 分别是 BC 、 CD 的中点，
∴ AB ＝ BC ＝ CD ＝ AD ＝ 6 ， BE ＝ CE ＝ CF ＝ DF ＝ 3 ，
，
，
＝ 6 2 － ×3×6 －
×3×6 －
×3×3
＝ ，
又 ∵
＝ ×3
× FM ，
即 ×3
× FM ＝
，解得 FM ＝
．
∵ ，
∴ 是等腰直角三角形， GM ＝ FM ＝
，
∴ ．
故选： C ．
【点睛】
本题考查直角三角形的相关计算，构造关于 GF 的直角三角形、利用勾股定理，是解题的关键．
2.
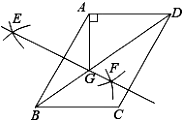
如图，在平行四边形 ABCD 中，对角线 BD ＝ 8 ，分别以点 A ， B 为圆心，以大于 AB 的长为半径画弧，两弧相交于点 E 和点 F ，作直线 EF ，交对角线 BD 于点 G ，连接 GA ， GA 恰好垂直于边 AD ，若 GA ＝ 3 ，则 AD 的长是（ ）
A ． 3 B ． 4 C ． 5 D ． 3
难度：
知识点：课题学习 最短路径问题
使用次数：120
【答案】
B
【解析】
【分析】
由作法知 EF 垂直平分 AB ，根据线段垂直平分线的性质得到 BG = GA =3 ，则 DG =5 ，根据勾股定理即可求解．
【详解】
解：由作图可知： EF 是线段 AB 的垂直平分线，
∴ BG = GA =3 ，
∴ DG = BD - BG =8-3=5 ，
∵ GA ⊥ AD ，
∴∠ GAD =90° ，
在 Rt △ ADG 中，由勾股定理，得
AD = =4 ，
故选： B ．
【点睛】
本题考查线段垂直平分线的尺规作法，线段垂直平分线的性质，勾股定理，熟练掌握线段垂直平分线的尺规作法＼线段垂直平分线的性质是解题的关键．
3.
△ ABC 中， ，
，高
，则 △ ABC 的面积为（ ）
A ． 66 B ． 126 C ． 54 或 44 D ． 126 或 66
难度：
知识点：勾股定理
使用次数：134
【答案】
D
【解析】
【分析】
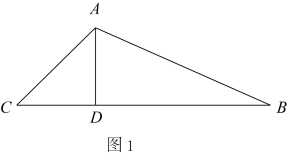
把三角形分为高在三角形内部和外部的两种情况，如图 1 ， 2 ，利用勾股定理求出 BC 的长，然后根据三角形面积公式求解即可．
【详解】
解：由题意知，分两种情况求解：
① 如图 1 ， 在
内部
在 中，由勾股定理得
在 中，由勾股定理得
∴
∴ ；
② 如图 2 ， 在
外部
在 中，由勾股定理得
在 中，由勾股定理得
∴
∴ ；
综上所述， 的面积为 66 或 126 ；
故选 D ．
【点睛】
本题考查了勾股定理的应用．解题的关键在于把三角形分为高在三角形内部和外部的两种情况．
4.
如图是我国汉代数学家赵爽在注解《周髀算经》时给出的 “ 勾股方圆图 ” （又称赵爽弦图），它是由四个全等的直角三角形（直角边分别为 a ， b ，斜边为 c ）与中间的一个小正方形拼成的一个大正方形．如果大正方形的面积为 11 ，小正方形的面积为 3 ，则 的值为（ ）
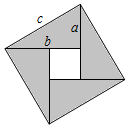
A ． 68 B ． 89 C ． 119 D ． 130
难度：
知识点：勾股定理
使用次数：178
【答案】
B
【解析】
【分析】
利用含 a ， b ， c 表示出大正方形和小正方形的面积，由两式相减可求得 ，再对
利用完全平方公式进行变形即可求得答案．
【详解】
解：大正方形的面积为： ，
小正方形的面积为： ，
由 得，
，即
，
，
故选 B ．
【点睛】
本题考查了勾股定理的应用、已知等式的值求多项式的值的问题。正方形的面积公式，把多项式化为已知多项式形的形式是解题的关键．
5.
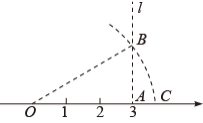
数学课本上有以下片段，其中点 C 表示的实数是（ ）
如图，在数轴上找出表示 3 的点 A ，则 ，过点 A 作直线 l 垂直于 OA ．在 l 上取点 B ，使
，以原点 O 为圆心．以 OB 为半径作弧，弧与数轴的交点 C ．
A ． B ． 4 C ．
D ．
难度：
知识点：实数
使用次数：108
【答案】
D
【解析】
【分析】
根据勾股定理可得 ，从而得到
，即可求解．
【详解】
解：根据题意得 ∶ OB = CO ， ，
∴ ，
∴ 点 C 表示的实数是 ．
故选： D
【点睛】
本题主要考查了勾股定理，实数与数轴，熟练掌握勾股定理，实数与数轴的关系是解题的关键．
本卷还有35题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
40
总体难度：
中等
难度统计
难度系数
数量
占比
中等
16
40.0%
容易
20
50.0%
基础
3
7.5%
偏难
1
2.5%
题型统计
大题类型
数量
占比
选择题
25
62.5%
填空题
15
37.5%
知识点统计
知识点
数量
占比
勾股定理
11
27.50%
课题学习 最短路径问题
2
5.0%
实数
1
2.5%
勾股定理的逆定理
4
10.0%
等腰三角形
6
15.0%
几何图形
2
5.0%
三角形全等的判定
4
10.0%
与三角形有关的线段
1
2.5%
角的平分线的性质
4
10.0%
平面直角坐标系
2
5.0%
平行线的性质
1
2.5%
二次根式的加减
1
2.5%
二次根式的乘除
1
2.5%
版权提示
该作品由: 用户张敏分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。