如图,射线 OM 上有 A 、 B 、 C 三点,满足 OA = 40cm , AB = 30cm , BC = 20cm .点 P 从点 O 出发,沿 OM 方向以 2cm/ 秒的速度匀速运动,点 Q 从点 C 出发在线段 CO 上向点 O 匀速运动,两点同时出发,当点 Q 运动到点 O 时,点 P , Q 停止运动.
( 1 )当点 P 与点 Q 都同时运动到线段 AB 的中点时,求点 Q 的运动速度;
( 2 )当 PA = 2PB 时,点 Q 运动到的位置恰好是线段 OB 的中点,求点 Q 的运动速度;
( 3 )自点 P 运动到线段 AB 上时,分别取 OP 和 AB 的中点 E 、 F ,求 的值.
![]()
( 1 )点 Q 的运动速度为 cm/s ;( 2 )点 Q 的运动速度为
cm/s 或
cm/s ;( 3 ) 2
【分析】
( 1 )设经过 ts ,点 P 与点 Q 都同时运动到线段 AB 的中点,根据线段中点的定义得到 BQ = 15cm ,求得 CQ = 35cm ,于是得到结论;
( 2 )设 Q 的速度为 v ,经过 ts 后,点 Q 运动到的位置恰好是线段 OB 的中点,点 O 对应数轴上的 0 ,点 A 对应数轴上的 40 ,点 B 对应数轴上的 70 ,点 C 对应数轴上的 90 ,点 P 对应数轴上的 2t ,点 Q 对应数轴上的 90 ﹣ vt ,根据题意列出方程即可求出 v 的值;
( 3 )设经过 ts 时,点 P 在 AB 之间,点 O 对应数轴上的 0 ,点 A 对应数轴上的 40 ,点 B 对应数轴上的 70 ,点 C 对应数轴上的 90 ,点 P 对应数轴上的 2t ,由于 OP 和 AB 的中点 E , F ,所以点 E 对应数轴上的 t ,点 F 对应数轴上的 55 ,从而可知 EF = 55 ﹣ t , AP = 2t ﹣ 40 , OB = 70 ,代入原式即可求出答案.
【详解】
解:( 1 ) ∵AB = 30cm ,
,
∴CQ = BC+BQ = 35cm ,
设经过 ts ,点 P 与点 Q 都同时运动到线段 AB 的中点,
∴OP = OA+PA = 40+15 = 55 ( cm ),
∴t = ( s ),
∴ 点 Q 的运动速度= 35÷ =
( cm/s );
答:点 Q 的运动速度为 cm/s ;
( 2 )设 Q 的速度为 v ,经过 ts 后,点 Q 运动到的位置恰好是线段 OB 的中点,点 O 对应数轴上的 0 ,点 A 对应数轴上的 40 ,点 B 对应数轴上的 70 ,点 C 对应数轴上的 90 ,
∴ 点 P 对应数轴上的 2t ,点 Q 对应数轴上的 90 ﹣ vt ,
∵ 点 Q 运动到的位置恰好是线段 OB 的中点,
∴ = 90 ﹣ vt ,
∴vt = 55 ,
∵2PB = PA ,
∴2|2t ﹣ 70| = |2t ﹣ 40| ,
∴ 解得: t = 50 或 t = 30 ,
当 t = 50s 时,
此时 v = ,
而点 Q 到达 O 点所需要时间为 s
50s ,
当 t = 30 时,
此时 v = ,
而点 Q 到达 O 点所需要的时间为
30s ,
综上所述,当 v = 或 v =
cm/s ;
( 3 )设经过 ts 时,点 P 在 AB 之间,
点 O 对应数轴上的 0 ,点 A 对应数轴上的 40 ,点 B 对应数轴上的 70 ,点 C 对应数轴上的 90 ,
∴ 点 P 对应数轴上的 2t ,
∵OP 和 AB 的中点 E , F ,
∴ 点 E 对应数轴上的 t ,点 F 对应数轴上的 55 ,
∴EF = 55 ﹣ t , AP = 2t ﹣ 40 , OB = 70 ,
∴ 原式= = 2 .
【点睛】
本题主要考查一元一次方程的应用,数形结合列出方程是解题的关键.
如图,射线 在钝角
的内部,且
分
,
平分
.
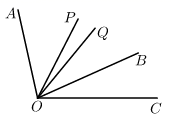
( 1 )当 与
重合时,求
得度数;
( 2 )若 ,求
的度数;
( 3 )若 ,求
的度数(用含 n 的代数式表示).
( 1 ) 120° ;( 2 ) 10° ;( 3 ) n°-90°
【分析】
( 1 )根据角平分线的定义得到 AOB=∠BOC= ∠AOC ,再结合 ∠AOB+∠AOC=180° ,可得 ∠AOC 的度数;
( 2 )根据 ∠AOC 得到 ∠AOB ,再根据角平分线的定义得到 ∠AOP=40° 和 ∠AOQ=50° ,从而求出 ∠POQ ;
( 3 )根据( 2 )中的方法和过程求解即可.
【详解】
解:( 1 )如图( 1 ),
∵OQ 平分 ∠AOC ,且点 Q 与点 B 重合,
∴∠AOB=∠BOC= ∠AOC ,
∵∠AOB+∠AOC=180° ,
∴ ∠AOC+∠AOC=180° ,
∴∠AOC=120° ;

( 2 )如图( 2 ),
∵∠AOC=100° ,
又 ∵∠AOB+∠AOC=180° ,
∴∠AOB=80° ,
∵OP 平分 ∠AOB ,
∴∠AOP=40° ,
∵OQ 平分 ∠AOC ,
∴∠AOQ=50° ,
∴∠POQ=∠AOQ-∠AOP=50°-40°=10° ;

( 3 ) ∵∠AOC=n° ,
∴∠AOB+∠AOC=180° ,
∴∠AOB=180°-n° ,
∵OQ 平分 ∠AOC ,
∴∠AOQ= ∠AOC=
,
∵OP 平分 ∠AOB ,
∴∠AOP= ∠AOB=
=
,
∴∠POQ=∠AOQ-∠AOP
=
= .
【点睛】
本题考查角平分线的定义,角的和差,余角和补角的意义,掌握角平分线的定义以及角的和差关系是正确解答的前提.
如图, 为直线
上一点,过点
作射线
,使
.将一直角三角尺的直角顶点放在
处.
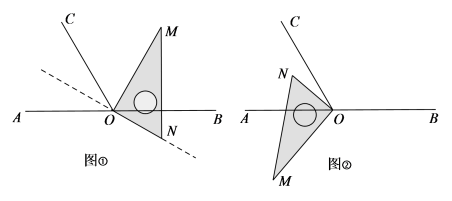
( 1 )当三角尺一边 在
的内部(图 ① ),且恰好平分
,此时直线
是否平分
?请说明理由;
( 2 )当三角尺一边 在
的内部(图 ② ),求
的值.
( 1 )直线 平分
,理由见解析;( 2 )
.
【分析】
( 1 )设 的反向延长线为
,由角平分线的性质可知
,由邻补角定义解得
,继而解得
,由此证明
即可解题;
( 2 )先计算 ,
,再计算
的值即可.
【详解】
解:( 1 )如图,设 的反向延长线为
,
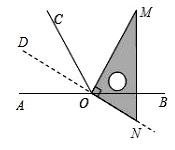
,
平分
,
,
,
,
即 ,
直线
平分
;
( 2 )如图,由于 ,
,
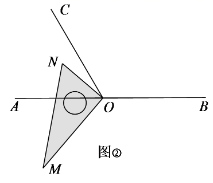
,
.
【点睛】
本题考查角平分线的性质、三角板有关的角的计算等知识,是重要考点,难度较易,掌握相关知识是解题关键.
如图,直线 AB 、 CD 相交于点 O , OE 平分 ∠AOD , ∠FOC=90° , ∠1=38° .求 ∠2 和 ∠3 的度数.
∠2=64° , ∠3=52° .
【分析】
利用平角、互补和角平分线的定义进行计算即可.
【详解】
解: ∵AB 为直线,
∴∠3+∠FOC+∠1=180° .
∵∠FOC=90° , ∠1=38° ,
∴∠3=180° - 90° - 38°=52° .
∵∠3 与 ∠AOD 互补,
∴∠AOD=180° - ∠3=128° .
∵OE 平分 ∠AOD ,
∴∠2= ∠AOD=64° .
【点睛】
本题考查了角的计算,掌握平角、补角及角平分线的定义,并利用数形结合的思想是解答此题的关键.
如图,已知线段 ,
,线段
在直线
上运动(点
在点
的左侧,点
在点
的左侧),若
.
( 1 )求线段 ,
的长;
( 2 )若点 ,
分别为线段
,
的中点,
,求线段
的长;
( 3 )当 运动到某一时刻时,点
与点
重合,点
是线段
的延长线上任意一点,下列两个结论: ①
是定值, ②
是定值,请选择你认为正确的一个并加以说明.
( 1 ) ,
;( 2 ) 9 ;( 3 ) ② 正确,
,见解析
【分析】
( 1 )利用两个非负数和为 0 ,可得每个非负数为 0 ,可求 ,
即可;
( 2 )分类考虑当点 在点
的右侧和点
在点
的左侧时,利用中点可求 AM , DN ,利用线段和差求 AD ,可求 MN=AD-AM-DN 即可;
( 3 )利用 PA=PC+AC , PB=PC-BC ,求出 PA+PB=2PC 即可.
【详解】
解:( 1 )由 ,
,
,
得 ,
,
所以 ,
;
( 2 )当点 在点
的右侧时,如图,

因为点 ,
分别为线段
,
的中点,
,
所以 ,
,
又因为 ,
所以 ,
当点 在点
的左侧时,如图,

因为点 ,
分别为线段
,
的中点,
所以 ,
,
所以
所以 .
综上,线段 的长为 9 ;
( 3 ) ② 正确,且 .理由如下:
因为点 与点
重合,所以
,
所以 ,所以
,
所以 .

【点睛】
本题考查非负数的性质,线段中点,线段和差,线段的比问题,掌握非负数的性质,线段中点,线段和差,线段的比,关键是利用线段和差 PA=PC+AC , PB=PC-BC ,求出 PA+PB=2PC .
本卷还有45题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。