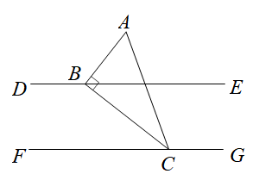
如图，直线 的顶点 B ， C 分别在 上，若 ，则 的大小为（ ）

A ． B ． C ． D ．

答案

C

【分析】先根据平行线的性质得到 ∠ EBC =∠ BCF =25° ，再利用互余得到 ∠ ABE =65° ．

【详解】解： ∵ ， ，

∴∠ EBC =∠ BCF =25°

∵∠ ABC =90° ，

∴∠ ABE =∠ ABC -∠ EBC =90°-25°=65° ．

故选： C ．

【点睛】本题考查了平行线的性质、余角和补角，掌握 “ 两直线平行，内错角相等 ” 是解题关键．