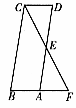
如图， AB CD ，点 G 、 F 分别为 AD 、 BD 的中点， GF 与 AC 交于点 E ，若 AB ＝ 5 ， CD ＝ 3 ，则 EF 的长是（　　）

A ． 4 B ． 3 C ． 1 D ．

答案

C

【分析】先用三角形中位线定理求出 GF 的长，再证明 △ AGE ∽△ ADC 求出 GE 的长即可求出 EF 的长．

【详解】解： ∵ 点 G 、 F 分别为 AD 、 BD 的中点，

∴ GF ＝ AB ＝ 2.5 ， GF AB ，

∵ AB CD ，

∴ GF CD ，

∴△ AGE ∽△ ADC ，

∴ ，

∴ GE ＝ CD ＝ 1.5 ，

∴ EF ＝ GF ﹣ GE ＝ 2.5 ﹣ 1.5 ＝ 1 ，

故选： C ．

【点睛】本题主要考查了相似三角形的性质与判定，三角形中位线定理，分别求出 GF ， GE 的长是解题的关键．