在平行四边形 ABCD 中，有两个内角的度数比为 1 ： 2 ，则这个平行四边形中较大的内角是（ ）

A ． 45° B ． 60° C ． 90° D ． 120°

答案

D

【分析】据平行四边形的性质得出 AB // CD ，推出 ∠ B +∠ C = 180° ，根据 ∠ B ∶∠ C = 1∶2 ，求出 ∠ C 即可．

【详解】如图：

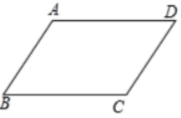
因为四边形 ABCD 是平行四边形

∴ AB // CD ，

∴∠ B +∠ C = 180° ，

又 ∠ B ： ∠ C =1∶2 ，

∴∠ C = ×180°= 120°

故选： D ．

【点睛】本题考查了平行线的性质和平行四边形的性质的应用，能熟练地运用性质进行计算是解此题的关键，题目比较典型，难度不大．