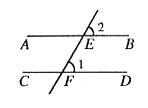
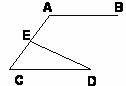
如图， 中， ， ， 于 E ，则 等于（ ）

A ． 20° B ． 30° C ． 50° D ． 60°

答案

C

【分析】在 Rt △ AEB 中，想办法求出 ∠ ABE 即可解决问题．

【详解】解： ∵ DB ＝ DC ，

∴∠ C ＝ ∠ DBC ＝ 70° ，

∴∠ CDB ＝ 180°−140° ＝ 40° ，

∵ 四边形 ABCD 为平行四边形，

∴ CD ∥ AB ，

∴∠ ABE ＝ ∠ CDB ＝ 40° ，

∵ AE ⊥ BD ，

∴∠ AEB ＝ 90° ，

∴∠ BAE ＝ 90°−40° ＝ 50° ．

故选： C ．

【点睛】本题考查平行四边形的性质、等腰三角形的性质．直角三角形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于基础题，中考常考题型．