如图，已知钝角三角形 ABC ，将 △ ABC 绕点 A 按逆时针方向旋转 110° 得到 ，连接 ，若 ，则 的度数为（ ）

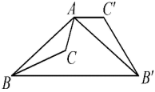
A ． 55° B ． 65° C ． 85° D ． 75°

答案

D

【解析】

【分析】

根据旋转的性质确定 ， ，根据三角形内角和定理，等边对等角求出 ，根据平行线的性质求出 ，最后根据角的和差关系即可求解．

【详解】

解： ∵△ ABC 绕点 A 按逆时针方向旋转 110° 得到 ，

∴ ， ．

∴ ．

∵ ，

∴ ．

∴ ．

故选： D ．

【点睛】

本题考查旋转的性质，三角形内角和定理，等边对等角，平行线的性质，角的和差关系，熟练掌握这些知识点是解题关键．