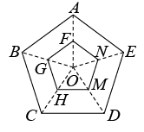
如图,五边形 ABCDE 是由五边形 FGHMN 经过位似变换得到的,点 O 是位似中心, F 、 G 、 H 、 M 、 N 分别是 OA 、 OB 、 OC 、 OD 、 OE 的中点,则五边形 ABCDE 与五边形 FGHMN 的面积比是( )
A . 2 : 1 B . 4 : 1 C . 5 : 1 D . 6 : 1
答案
B
【解析】
【分析】
由题意可知五边形 ABCDE 与五边形 FGHMN 相似 ,再 由面积比是相似比的平方,可得答案.
【详解】
解:由题意可得:五边形 ABCDE 与五边形 FGHMN 相似,且相似比为 2 : 1
面积比是相似比的平方
五边形 ABCDE 与五边形 FGHMN 的面积比是 4 : 1
故选 B
【点睛】
此题考察的知识点有:位似、相似、中点的性质、相似比和面积比;面积比是相似比的平方是解题关键.