一块含 角的直角三角板和直尺如图放置，若 ，则 的度数为（ ）

A ． B ． C ． D ．

答案

B

【分析】

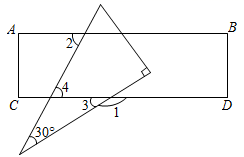
先根据邻补角的定义得出 ∠3=180°-∠1=33°27′ ，再根据平行线的性质得到 ∠4=∠2 ，然后根据三角形的外角的性质即可得到结论．

【详解】

解： ∵ ，

∴∠3=180°-∠1=33°27′ ，

∴∠4=∠3+30°=63°27′ ，

∵ AB ∥ CD ，
∴∠2=∠4=63°27′ ，
故选： B ．

【点睛】

本题考查了平行线的性质，三角形外角性质的应用，能求出 ∠3 的度数是解此题的关键，注意：两直线平行，内错角相等．