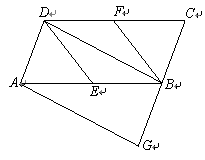
如图,在 ▱ ABCD 中, AC , BD 交于点 O ,且 AO = BO .
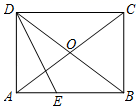
( 1 )求证:四边形 ABCD 是矩形;
( 2 ) ∠ ADB 的角平分线 DE 交 AB 于点 E ,当 AD = 3 , tan∠ CAB = 时,求 AE 的长.
答案
( 1 )见解析;( 2 ) .
【分析】
(1) 由平行四边形性质和已知条件得出 AC = BD ,即可得出结论;
(2) 过点 E 作 EG ⊥ BD 于点 G ,由角平分线的性质得出 EG = EA .由三角函数定义得出 AB = 4 , sin∠ CAB = sin∠ ABD = ,设 AE = EG = x ,则 BE = 4 ﹣ x ,在 Rt△ BEG 中,由三角函数定义得出
,即可得出答案.
【详解】
(1) 证明: ∵ 四边形 ABCD 是平行四边形,
∴ AC = 2 AO , BD = 2 BO .
∵ AO = BO ,
∴ AC = BD .
∴ 平行四边形 ABCD 为矩形.
(2) 过点 E 作 EG ⊥ BD 于点 G ,如图所示:
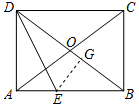
∵ 四边形 ABCD 是矩形,
∴∠ DAB = 90° ,
∴ EA ⊥ AD ,
∵ DE 为 ∠ ADB 的角平分线,
∴ EG = EA .
∵ AO = BO ,
∴∠ CAB = ∠ ABD .
∵ AD = 3 , tan∠ CAB = ,
∴tan∠ CAB = tan∠ ABD = =
.
∴ AB = 4 .
∴ BD = , sin∠ CAB = sin∠ ABD =
.
设 AE = EG = x ,则 BE = 4 ﹣ x ,
在 △ BEG 中, ∠ BGE = 90° ,
∴sin∠ ABD = .
解得: x = ,
∴ AE = .
故答案为: .
【点睛】
本题考查了矩形的判定与性质、角平分线的性质、勾股定理、三角函数定义等知识;熟练掌握矩形的判定与性质和三角函数定义是解题的关键.