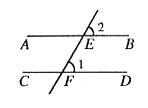
如图，将一副三角尺按图中所示位置摆放，点 在 上，其中 ， ， ， ， ，则 的度数是（ ）

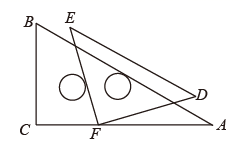
A ． B ． C ． D ．

答案

A

【分析】

设 AB 与 EF 交于点 M ，根据 ，得到 ，再根据三角形的内角和定理求出结果．

【详解】

解：设 AB 与 EF 交于点 M ，

∵ ，

∴ ，

∵ ， ，

∴ ，

∴ ,

∵ ,

∴ = ，

故选： A ．

．

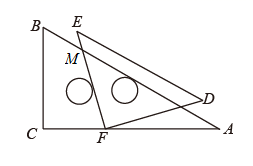【点睛】

此题考查平行线的性质，三角形的内角和定理，熟记平行线的性质并应用是解题的关键．