综合与实践
操作发现：
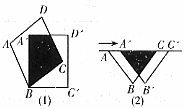
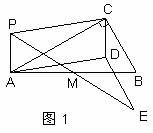
如图1和图2,已知点P为正方形ABCD的边AD和CD上的一个动点(点A,D,C除外), 作射线BP,作AE丄BP于点E,CF丄BP于点F,DG丄BP于点G.
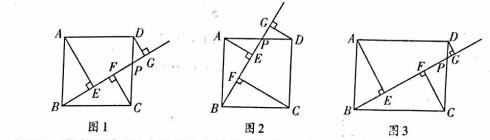
(1)如图1,当点P在CD上(点C, D除外)运动时，求证:AE=CF+DG;
(2)如图2,当点P在AD上(点A,D除外)运动时，清宜接写岀线段AE,CF,DG之间的数量关系；
拓广探索：
(3)在(1)的条件下，找出与DG相等的线段,并说明理由；
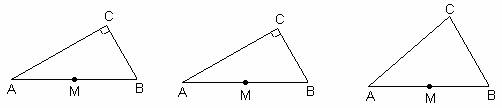
(4)如图3,若点P为矩形ABCD的边CD上一点，作射线BP,作AE丄BP于点E,CF丄BP 于点F,DG丄BP于点G.若CD=2BE=6,
很,则DG= ▲ .
答案
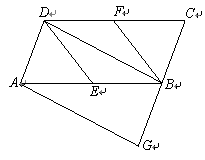
解：（1）证明：如答图，过点D作DH⊥CF交CF的延长线于点H，
则∠CHD=∠AEB=90°.
∵四边形ABCD为正方形，
∴AB=CD，AB⫽CD. ………………………………………… 1分
∴∠ABE=∠CPF．
∵AE⊥BP，CF⊥BP，DG⊥BP，
∴∠AEB=∠CFP=∠DGF=90°.
∴∠ABE+∠BAE=∠CPF+∠DCH =90°.
∴∠BAE=∠DCH.………………………………………………………… 2分
在△ABE和△CDH中，
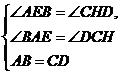
∴△ABE≌△CDH（AAS）.
∴AE=CH. ………………………………………………………… 3分
∵∠CHD=∠HFG=∠DGF=90°，
∴四边形HFGD为矩形.
∴HF=DG，
∴AE=CH=CF+HF=CF+DG. …………………………………………4分
(2)线段AE，CF，DG之间的数量关系是CF =AE+DG. ……………… 6分
(3)与DG相等的线段是EF. ………………………………… 7分
理由如下：如图1，
∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°.
∵AE⊥BP，
∴∠AEB=90°.
∴∠ABE+∠BAE=∠ABE+∠CBF =90°.
∴∠BAE=∠CBF . ………………………………………………………… 8分
在△ABE和△BCF中，
,
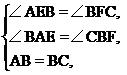∴△ABE≌△BCF（AAS）.
∴AE=BF，BE=CF.
∴AE=BF=BE+EF=CF+EF. ……………………………………………… 9分
由（1），得AE= CF+DG.
∴DG=EF. …………………………………………………………… 10分
(4)
……………………………………………………………12分
