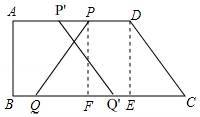
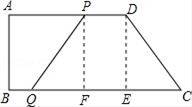
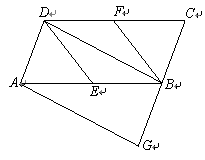
如图,在在四边形ABCD中,AD![]() ∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)BC= cm;
(2)当t= 秒时,四边形PQBA成为矩形.
(3)当t为多少时,PQ=CD?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.

答案
【解答】解:根据题意得:PA=2t,CQ=3t,则PD=AD﹣PA=12﹣2t,
(1)如图,过D点作DE⊥BC于E,则四边形ABED为矩形,
∴DE=AB=8cm,AD=BE=12cm,
在Rt△CDE中,∵∠CED=90°,DC=10cm,DE=8cm,
∴EC=![]() =6cm,
=6cm,
∴BC=BE+EC=18cm.
故答案为18;
(2)∵AD∥BC,∠B=90°
∴当PA=BQ时,四边形PQBA为矩形,
即2t=18﹣3t,
解得t=![]() 秒,
秒,
故当t=![]() 秒时,四边形PQBA为矩形;
秒时,四边形PQBA为矩形;
故答案为![]() ;
;
(3)
①当P'Q'∥CD时,如图,
∵AD∥BC,
∴四边形CDP'Q'是平行四边形,
∴P'Q'=CD,DP'=CQ',
∴12﹣2t=3t,
∴t=![]() 秒,
秒,
②如图,梯形PDCQ是等腰梯形时,PQ=CD,
易证,四边形PDEF是矩形,
∴EF=DP=12﹣2t,
易证,△CDE≌△QPF,
∴FQ=CE=6,
∴CQ=FQ+EF+CE=6+12﹣2t+6=3t,
∴t=![]()
(4)△DQC是等腰三角形时,分三种情况讨论:
①当QC=DC时,即3t=10,
∴t=![]() ;
;
②当DQ=DC时,![]() =6,
=6,
∴t=4;
③当QD=QC时,3t•![]() =5,
=5,
∴t=![]() .
.
故存在t,使得△DQC是等腰三角形,此时t的值为![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.