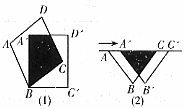
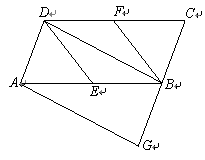
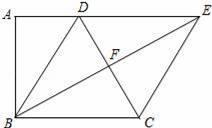
如图，在梯形ABCD中，AD∥BC，∠A=∠ABC=90°，且AD=
CD．将梯形ABCD沿对角线BD折叠，点A恰好落在CD边的点F上，延长BF交AD延长线于点E，连接EC．
（1）求证：△DEF≌△CBF；
（2）判断四边形BCED是什么特殊四边形？说明理由；
（3）求∠ADC的度数．（直接写结论，不用证明）
答案
【考点】四边形综合题．
【分析】（1）利用折叠和AD=
CD，得出DF=CF，利用ASA得出△DEF≌△CBF；
（2）先利用DF=FC，EF=BF，得出四边形BCED是平行四边形，再进一步证明△DBF≌△CFE，得出DB=DE，证得四边形BCED是菱形；
（3）利用折叠得出∠ADB=∠CDB，利用菱形得出∠CDB=∠CDE，由此得出∠ADB=∠CDB=∠CDE=60°，得出∠ADC=120°．
【解答】（1）证明：∵梯形ABCD沿对角线BD折叠，点A恰好落在CD边的点F上，
∴∠DFB=∠A=90°，AD=DF，
∵AD=
CD，
∴DF=CD，
∴DF=CF，
∵AD∥BC，
∴∠FDE=∠FCB，
在△DEF和△CBF中，
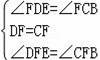
∴△DEF≌△CBF；
（2）四边形BCED是菱形．
理由：∵△DEF≌△CBF，
∴DF=FC，EF=BF，
∴四边形BCED平行四边形，
在△DBF和△CFE中，
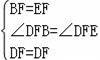
∴△DBF≌△CFE，
∴DB=DE，
∴四边形BCED是菱形．
（3）∠ADC=120°．
∵折叠，
∴∠ADB=∠CDB，
∵四边形BCED是菱形，
∴∠CDB=∠CDE，
∴∠ADB=∠CDB=∠CDE=60°，
∴∠ADC=120°．
【点评】此题综合考查三角形全等的判定与性质，折叠的性质，菱形的判定，注意已知条件与所求问题之间的联系，灵活运用知识之间的联系解决问题．
