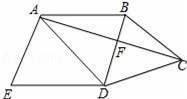
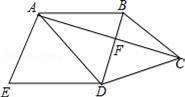
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.

答案
【考点】平行四边形的判定与性质.
【分析】(1)根据已知和角平分线的定义证明∠ADE=∠BAD,得到DE∥AB,又AE∥BD,根据两组对边分别平行的四边形是平行四边形证明即可;
(2)设BF=x,根据勾股定理求出x的值,再根据勾股定理求出AF,根据AC=2AF得到答案
【解答】(1)证明:∵AE⊥AC,BD垂直平分AC,
∴AE∥BD,
∵∠ADE=∠BAD,
∴DE∥AB,
∴四边形ABDE是平行四边形;
(2)解:∵DA平分∠BDE,
∴∠BAD=∠ADB,
∴AB=BD=5,
设BF=x,
则52﹣x2=62﹣(5﹣x)2,
解得,x=![]()
![]() ,
,
∴AF=![]()
![]() =
=![]()
![]() ,
,
∴AC=2AF=![]()
![]() .
.

【点评】本题考查的是平行四边形的判定和性质,掌握平行四边形的判定定理和性质定理以及勾股定理是解题的关键.