2020江苏八年级上学期苏科版初中数学期中考试138077
初中
整体难度：中等
2020-12-16
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
日常生活中，我们会看到很多标志，在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．
B．
C．
D．
难度：
知识点：轴对称
使用次数：111
【答案】
A
【分析】
结合轴对称图形的概念进行求解， 如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．
【详解】
A. 是轴对称图形，本选项符合题意；
B. 不是轴对称图形，本选项不符合题意；
C. 不是轴对称图形，本选项不符合题意；
D. 不是轴对称图形，本选项不符合题意.
故选A.
【点睛】
本题考查的是轴对称图形，熟练掌握轴对称图形的定义是解题的关键.
2.
4的算术平方根是（ ）
A．±4 B．4 C．±2 D．2
难度：
知识点：平方根
使用次数：135
【答案】
D
【分析】
如果一个正数x的平方等于a，即x2=a（x>0），那么这个正数x 叫做a的算术平方根.
【详解】
解：4的算术平方根是2.
故选D.
【点睛】
本题考查了算术平方根的定义，熟练掌握相关定义是解题关键.
3.
如图，DABC@DADE，ÐB=100°，ÐBAC=30°，那么ÐAED=（ ）
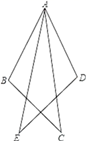
A．30° B．40° C．50° D．60°
难度：
知识点：全等三角形
使用次数：150
【答案】
C
【分析】
先在
中求得
的度数，再根据
得到
即可.
【详解】
解：
,
，
.
故选:
.
【点睛】
本题主要考查全等三角形的判定，熟练掌握判定定理是解答关键.
4.
如图，两个正方形的面积分别为64和49，则
等于（ ）
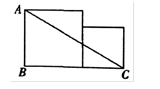
A．15 B．17 C．23 D．113
难度：
知识点：勾股定理
使用次数：136
【答案】
B
【解析】
试题解析：∵两个正方形的面积分别是64和49，
∴AB=BD=8，DC=7，
根据勾股定理得：AC=
=17．
故选B．
5.
到三角形三个顶点距离相等的点是（ ）
A．三条角平分线的交点 B．三边中线的交点
C．三边上高所在直线的交点 D．三边的垂直平分线的交点
难度：
知识点：课题学习 最短路径问题
使用次数：165
【答案】
D
【分析】
根据垂直平分线的性质定理的逆定理即可做出选择．
【详解】
∵到一条线段两端点的距离相等的点在这条线段的垂直平分线上，
∴到三角形三个顶点距离相等的点是三边的垂直平分线的交点，
故选：D．
【点睛】
本题考查了线段垂直平分线，理解线段垂直平分线的性质的逆定理是解答的关键．
本卷还有23题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
28
总体难度：
中等
难度统计
难度系数
数量
占比
中等
15
53.57%
基础
3
10.71%
容易
7
25.0%
偏难
3
10.71%
题型统计
大题类型
数量
占比
选择题
10
35.71%
填空题
8
28.57%
解答题
10
35.71%
知识点统计
知识点
数量
占比
轴对称
4
14.28%
平方根
3
10.71%
全等三角形
1
3.57%
勾股定理
3
10.71%
课题学习 最短路径问题
2
7.14%
勾股定理的逆定理
1
3.57%
等腰三角形
4
14.28%
三角形全等的判定
2
7.14%
画轴对称图形
2
7.14%
与三角形有关的线段
1
3.57%
特殊的平行四边形
2
7.14%
角的平分线的性质
1
3.57%
实数
1
3.57%
与三角形有关的角
1
3.57%
版权提示
该作品由: 用户朱玉周分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。