初中数学吉林省2020年中考数学真题含答案解析.doc

学科首页试卷详情

2020吉林人教版初中数学中考真题121372

初中

整体难度：中等

2020-11-05

题号

一

二

三

四

五

评分

一、解答题 (共9题)

添加该题型下试题

如图，在平面直角坐标系中，抛物线与轴正半轴交于点，且点的坐标为，过点作垂直于轴的直线．是该抛物线上的任意一点，其横坐标为，过点作于点；是直线上的一点，其纵坐标为，以，为边作矩形．

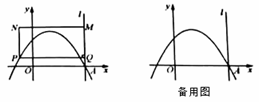
（1）求的值．

（2）当点与点重合时，求的值．

（3）当矩形是正方形，且抛物线的顶点在该正方形内部时，求的值．

（4）当抛物线在矩形内的部分所对应的函数值随的增大而减小时，直接写出的取值范围．

难度：

知识点：二次函数与一元二次方程

使用次数：170

复制

详情

加入组卷

【答案】

（1）；（2）；（3）；（4）或．

【解析】

（1）将A点坐标代入函数解析式即可求得b的值；

（2）分别表示出P、Q、M的坐标，根据Q、M的横坐标相同，它们重合时纵坐标也相同，列出方程求解即可；

（3）分别表示出PQ和MQ的长度，根据矩形是正方形时，即可求得m的值，再根据顶点在正方形内部，排除不符合条件的m的值；

（4）分，，，四种情况讨论，结合图形分析即可．

【详解】

解：（1）将点代入

得，

解得b=1,；

（2）由（1）可得函数的解析式为，

∴,

∵于点，

∴,

∵是直线上的一点，其纵坐标为，

∴，

若点与点重合，则

，

解得；

（3）由（2）可得，，

当矩形是正方形时，

即，

即或，

解得，

又，

∴抛物线的顶点为(1，2)，

∵抛物线的顶点在该正方形内部，

∴P点在抛物线对称轴左侧，即，且M点的纵坐标大于抛物线顶点的纵坐标，即，

解得，故m的值为；

（4）①如下图

当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该小于P点纵坐标，且P点应该在x轴上侧，

即且，

解得，

∴，

②如下图

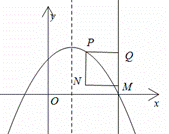
当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该小于P点纵坐标，

即，解得，

∴；

③当时，P点和M点都在直线x=3上不构成矩形，不符合题意；

④如下图

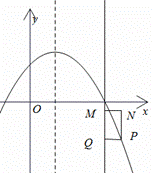
当时，若抛物线在矩形内的部分所对应的函数值随的增大而减小，

则M点的纵坐标应该大于P点纵坐标，

即，解得或，

故，

综上所述或．

【点睛】

本题考查二次函数综合，正方形的性质定理，求二次函数解析式．能分别表示出M、P、Q的坐标并结合图形分析是解决此题的关键，注意分类讨论．

某种机器工作前先将空油箱加满，然后停止加油立即开始工作，当停止工作时，油箱中油量为．在整个过程中，油箱里的油量（单位：）与时间（单位：）之间的关系如图所示．

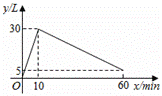
（1）机器每分钟加油量为_____，机器工作的过程中每分钟耗油量为_____．

（2）求机器工作时关于的函数解析式，并写出自变量的取值范围．

（3）直接写出油箱中油量为油箱容积的一半时的值．

难度：

知识点：课题学习选择方案

使用次数：175

复制

详情

加入组卷

【答案】

（1）3，；（2），；（3）5或40．

【解析】

（1）根据加油量为即可得；根据时剩余油量为即可得；

（2）根据函数图象，直接利用待定系数法即可得；

（3）先求出机器加油过程中的关于的函数解析式，再求出时，两个函数对应的x的值即可．

【详解】

（1）由函数图象得：机器每分钟加油量为

机器工作的过程中每分钟耗油量为

故答案为：3，；

（2）由函数图象得：当时，机器油箱加满，并开始工作；当时，机器停止工作

则自变量的取值范围为，且机器工作时的函数图象经过点

设机器工作时关于的函数解析式

将点代入得：

解得

则机器工作时关于的函数解析式；

（3）设机器加油过程中的关于的函数解析式

将点代入得：

解得

则机器加油过程中的关于的函数解析式

油箱中油量为油箱容积的一半时，有以下两种情况：

①在机器加油过程中

当时，，解得

②在机器工作过程中

当时，，解得

综上，油箱中油量为油箱容积的一半时的值为5或40．

【点睛】

本题考查了函数图象、利用待定系数法求一次函数和正比例函数的解析式等知识点，从函数图象中正确获取信息是解题关键．

年月线上授课期间，小莹、小静和小新为了解所在学校九年级名学生居家减压方式情况，对该校九年级部分学生居家减压方式进行抽样调查，将居家减压方式分为（享受美食）、（交流谈心）、（室内体育活动）、（听音乐）和（其他方式）五类，要求每位被调查者选择一种自己最常用的减压方式．他们将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．