2022-2023学年度初中数学图像法确定一元二次方程的近似根练习题含解析
初中
整体难度：中等
2022-08-31
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
方程 的解个数是（ ）
A ． 0 B ． 1 C ． 2 D ． 3
难度：
知识点：二次函数与一元二次方程
使用次数：181
【答案】
D
【分析】设 ，
，然后作出函数图象即可得出结果．
【详解】解：设 ，
，
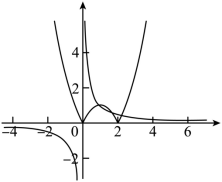
两个函数图象如图所示，有三个交点，
∴ 方程有三个解，
故选： D ．
【点睛】题目主要考查利用函数图象求方程的解，理解题意，准确作出函数图象是解题关键．
2.
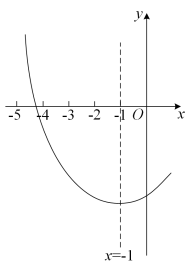
小颖用计算器探索方程 ax 2 + bx + c ＝ 0 的根，她作出如图所示二次函数 y ＝ ax 2 + bx + c 的图象，并求得一个近似根为 x ＝﹣ 4.3 ，则方程的另一个近似根为（ ）（精确到 0.1 ）
A ． x ＝ 4.3 B ． x ＝ 3.3 C ． x ＝ 2.3 D ． x ＝ 1.3
难度：
知识点：二次函数与一元二次方程
使用次数：183
【答案】
C
【分析】根据抛物线与 x 轴的一个交点为（﹣ 4.3 ， 0 ），又抛物线的对称轴为： x ＝﹣ 1 ，即可求解．
【详解】解： ∵ 抛物线与 x 轴的一个交点为（﹣ 4.3 ， 0 ），又抛物线的对称轴为： x ＝﹣ 1 ，
∴ 另一个交点坐标为：（ 2.3 ， 0 ），
则方程的另一个近似根为 x ＝ 2.3 ，
故选： C ．
【点睛】本题考查了根据二次函数图象求方程的近似根，掌握抛物线的对称性是解题的关键．
3.
根据表格中二次函数 y ＝ ax 2 + bx + c 的自变量 x 与函数值 y 的对应值，可以判断方程 ax 2 + bx + c ＝ 0 的一个解 x 的范围是（ ）
| x | 0 | 0.5 | 1 | 1.5 | 2 |
| y ＝ ax 2 + bx + c | | | 1 | 3.5 | 7 |
A ． 0 ＜ x ＜ 0.5 B ． 0.5 ＜ x ＜ 1
C ． 1 ＜ x ＜ 1.5 D ． 1.5 ＜ x ＜ 2
难度：
知识点：二次函数与一元二次方程
使用次数：245
【答案】
B
【分析】利用二次函数和一元二次方程的性质．
【详解】解：观察表格可知：当 x =0.5 时， y =-0.5 ；当 x =1 时， y =1 ，
∴ 方程 ax 2 + bx + c =0 （ a ≠0 ， a ， b ， c 为常数）的一个解 x 的范围是 0.5 ＜ x ＜ 1 ．
故选： B ．
【点睛】本题考查了用图象法求一元二次方程的近似根，解题的关键是找到 y 由正变为负时，自变量的取值即可．
4.
如表，是二次函数 的自变量 x 与函数值 y 的几组对应值．那么方程
的一个近似解是（ ）
| x | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| y | -1.49 | -1 | -0.49 | 0.04 | 0.59 | 1.16 |
A ． 1 B ． 1.1 C ． 1.2 D ． 1.3
难度：
知识点：二次函数与一元二次方程
使用次数：280
【答案】
C
【分析】由表格可得抛物线与 轴的一个交点在
和
之间且距离
较近，进而求解．
【详解】解：由表格可得 时，
，
时，
，
的一个解在 1.1 与 1.2 之间，
，
的一个近似解是 1.2 ，
故选： C ．
【点睛】本题考查二次函数图象上点的坐标特征，解题的关键是掌握二次函数与方程的关系．
5.
在二次函数 y ＝ ax 2 + bx + c 中，函数 y 与自变量 x 的部分对应值如表，则方程 ax 2 + bx + c ＝ 0 的一个解 x 的范围是（ ）
| x | … | 1 | 1.1 | 1.2 | 1.3 | 1.4 | … |
| y | … | | | 0.04 | 0.59 | 1.16 | … |
A ． 1 ＜ x ＜ 1.1 B ． 1.1 ＜ x ＜ 1.2 C ． 1.2 ＜ x ＜ 1.3 D ． 1.3 ＜ x ＜ 1.4
难度：
知识点：二次函数与一元二次方程
使用次数：185
【答案】
B
【分析】根据表格中自变量与函数的值的变化情况得出当 y =0 时相应的自变量的取值范围即可．
【详解】由表格中数据可知，当 x ＝ 1.1 时， y ＝－ 0.49.
当 x ＝ 1.2 时， y ＝ 0.04
于是可得，当 y ＝ 0 时，相应的自变量 x 的取值范围为 1.1 ＜ x ＜ 1.2
故选 B
【点睛】本题考查了用图像法求一元二次方程的近似根，解题的关键是找到 y 由正变为负时自变量的取值即可．
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
中等
18
51.42%
容易
16
45.71%
偏难
1
2.85%
题型统计
大题类型
数量
占比
选择题
10
28.57%
填空题
10
28.57%
解答题
15
42.85%
知识点统计
知识点
数量
占比
二次函数与一元二次方程
23
65.71%
二次函数的图象和性质
3
8.57%
函数
7
20.0%
课题学习 选择方案
1
2.85%
有理数
1
2.85%
版权提示
该作品由: 用户pengzhe分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。