如图，直线c与直线以a、b相交，且a∥b，若
1=55，则2的度数是（ ）
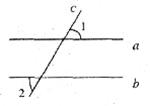
A．35 B．45 C．55 D．65
答案
C
如图，直线c与直线以a、b相交，且a∥b，若1=55，则2的度数是（ ）
A．35 B．45 C．55 D．65
C
平行公理：过直线外一点有且只有一条直线与已知直线平行。
推论（平行线的传递性）：平行同一直线的两直线平行。
∵a∥c，c ∥b
∴a∥b。
平行线的性质：
1. 两条平行被第三条直线所截，同位角相等。
简单说成：两直线平行，同位角相等。
2. 两条平行线被第三条直线所截，内错角相等。
简单说成：两直线平行，内错角相等。
3 . 两条平行线被第三条直线所截，同旁内角互补。
简单说成：两直线平行，同旁内角互补。
登录并加入会员可无限制查看知识点解析
B
D