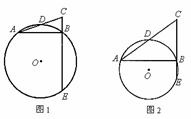
平行四边形 ，若 为 中点， 交 于点 ，连接 ．

(1) 若 ，

① 证明 为菱形；

② 若 ， ，求 的长．

(2) 以 为圆心， 为半径， 为圆心， 为半径作圆，两圆另一交点记为点 ，且 ．若 在直线 上，求 的值．

答案

(1)① 见解析； ②

(2)

【分析】（ 1 ） ① 连接 AC 交 BD 于 O ，证 △ AOE ≌ △ COE (SSS) ，得 ∠ AOE =∠ COE ，从而得 ∠ COE =90° ，则 AC ⊥ BD ，即可由菱形的判定定理得出结论；

② 先证点 E 是 △ ABC 的重心，由重心性质得 BE =2 OE ，然后设 OE = x ，则 BE =2 x ，在 Rt △ AOE 中，由勾股定理，得 OA ² = AE ² - OE ² =3 ² - x ² =9- x ² , 在 Rt △ AOB 中，由勾股定理，得 OA ² = AB ² - OB ² =5 ² -(3 x ) ² =25-9 x ² , 从而得 9- x ² =25-9 x ² ，解得： x = , 即可得 OB =3 x =3 ，再由平行四边形性质即可得出 BD 长；

（ 2 ）由 ⊙ A 与 ⊙ B 相交于 E 、 F ，得 AB ⊥ EF ，点 E 是 △ ABC 的重心，又 在直线 上，则 CG 是 △ ABC 的中线，则 AG = BG = AB ，根据重心性质得 GE = CE ＝ AE ， CG = CE + GE = AE ，在 Rt △ AGE 中，由勾股定理，得 AG ² = AE ² - GE = AE ² -( AE ) ² = AE ² , 则 AG = AE , 所以 AB =2 AG = AE ，在 Rt △ BGC 中，由勾股定理，得 BC ² = BG ² + CG ² = AE ² + （ AE ） ² =5 AE ² ，则 BC = AE ，代入即可求得 的值．

【详解】（ 1 ） ① 证明：如图，连接 AC 交 BD 于 O ，

∵ 平行四边形 ，

∴ OA = OC ，

∵ AE = CE ， OE = OE ，

∴△ AOE ≌ △ COE (SSS) ，

∴∠ AOE =∠ COE ，

∵∠ AOE +∠ COE =180° ，

∴∠ COE =90° ，

∴ AC ⊥ BD ，

∵ 平行四边形 ，

∴ 四边形 是菱形；

②∵ OA = OC ，

∴ OB 是 △ ABC 的中线，

∵ 为 中点，

∴ AP 是 △ ABC 的中线，

∴ 点 E 是 △ ABC 的重心，

∴ BE =2 OE ，

设 OE = x ，则 BE =2 x ，

在 Rt △ AOE 中，由勾股定理，得 OA ² = AE ² - OE ² =3 ² - x ² =9- x ² ,

在 Rt △ AOB 中，由勾股定理，得 OA ² = AB ² - OB ² =5 ² -(3 x ) ² =25-9 x ² ,

∴9- x ² =25-9 x ² ，

解得： x = ,

∴ OB =3 x =3 ，

∵ 平行四边形 ，

∴ BD =2 OB =6 ；

（ 2 ）解：如图，

∵⊙ A 与 ⊙ B 相交于 E 、 F ，

∴ AB ⊥ EF ，

由（ 1 ） ② 知点 E 是 △ ABC 的重心，

又 在直线 上，

∴ CG 是 △ ABC 的中线，

∴ AG = BG = AB ， GE = CE ，

∵ CE = AE ，

∴ GE = AE ， CG = CE + GE = AE ，

在 Rt △ AGE 中，由勾股定理，得

AG ² = AE ² - GE = AE ² -( AE ) ² = AE ² ,

∴ AG = AE ,

∴ AB =2 AG = AE ，

在 Rt △ BGC 中，由勾股定理，得

BC ² = BG ² + CG ² = AE ² + （ AE ） ² =5 AE ² ，

∴ BC = AE ，

∴ ．

【点睛】本题考查平行四边形的性质，菱形的判定，重心的性质，勾股定理，相交两圆的公共弦的性质，本题属圆与四边形综合题目，掌握相关性质是解题的关键，属是考常考题目．