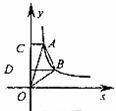
如图，在平面直角坐标系中，四边形 ABCD ， A 在 y 轴的正半轴上， B ， C 在 x 轴上， AD // BC ， BD 平分 ，交 AO 于点 E ，交 AC 于点 F ， ．若 OB ， OC 的长分别是一元二次方程 的两个根，且 ．

请解答下列问题：

(1) 求点 B ， C 的坐标；

(2) 若反比例函数 图象的一支经过点 D ，求这个反比例函数的解析式；

(3) 平面内是否存在点 M ， N （ M 在 N 的上方），使以 B ， D ， M ， N 为顶点的四边形是边长比为 的矩形？若存在，请直接写出在第四象限内点 N 的坐标；若不存在，请说明理由．

答案

(1) ， C （ 2 ， 0 ）

(2)

(3) 存在， N ₁ （ ， ）， N ₂ （ -9 ， 12 ）， N ₃ （ ， ）， ， ， ．

【分析】（ 1 ）解方程得出方程的解，即可确定点 B ， C 的坐标；

（ 2 ）首先证明 ∠ AFB ＝ ∠ AOB ＝ 90° ，再证明 AB = BC =5 ，由 得 ，从而得 ，即可得到 AD = AD =5 ，再由勾股定理求出 AO =4 ，得出点 D 的坐标即可求出反比例函数解析式；

（ 3 ）如图，分两种情况讨论求解即可．

【详解】（ 1 ）解：由 解得 ， ．

∵ OB ， OC 的长分别是方程的两个根，且 OB > OC ，

∴ ， ．

∴ ， C （ 2 ， 0 ）．

（ 2 ）解： ∵ AO ⊥ BC ，

∴∠ AOB ＝ 90° ．

∵∠ CAO ＝ ∠ DBC ， ，

∴∠ AFB ＝ ∠ AOB ＝ 90° ．

∵ BD 平分 ∠ ABC ，

∴∠ ABD ＝ ∠ DBC ．

∵∠ AFB ＝ 90° ，

∴∠ BAC ＝ ∠ BCA ．

∴ ．

∵ ，

∴ ，

∴ ．

∴ ．

∵ 在 Rt △ ABO 中， ．

∴ D （ 5 ， 4 ）．

∴ 反比例函数解析式为 ．

（ 3 ）解：如下图，过点 D 作 DQ ⊥ x 轴于点 Q ，过点 作 轴于点 ,

∴

∵ 四边形 是矩形，

∴

∴

又

∴

∴

∵

∴

∴

∴ 点 （ ， ），

同理可求出 N ₂ （ -9 ， 12 ）， N ₃ （ ， ），

② 如图，过点 D 作 DE ⊥ x 轴于点 E ，过点 WT 于点 F ，设 与 x 轴交于点 G ，

∴

又

∴

∵ BD 是圆的直径，

∴ 点 E 在圆上，

∴

∴

∴

∵ DE =4 ， BE =3+5=8 ，

∴

又 ，

设

由勾股定理得，

∴ ，解得，

∴

设 GE = x ，则 BG =8- x ，代入比例式得，

∴

在 Rt 中，

∴

解得， （舍去）

∴ BG =

∵

∴

由勾股定理可得， BF =

∴

∴

同理可得 ，

综上，点 N 的坐标为： N ₁ （ ， ）， N ₂ （ -9 ， 12 ）， N ₃ （ ， ）， ， ， ．

【点睛】本题主要考查了坐标与图形，求反比例函数解析式，相似三角形的判定与性质以及圆周角定理等知识，正确作出辅助线是解答本题的关键