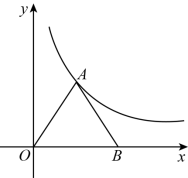
如图，等边三角形 OAB ，点 B 在 x 轴正半轴上， ，若反比例函数 图象的一支经过点 A ，则 k 的值是（ ）

A ． B ． C ． D ．

答案

D

【分析】过点 A 作 AC ⊥ x 轴于点 C ，则可根据勾股定理和三角形的面积求出 OC 和 OA 的长度，即可得出点 A 的坐标，将点 A 坐标代入反比例函数表达式即可求出 k ．

【详解】

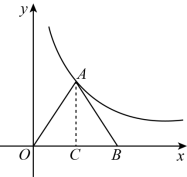
过点 A 作 AC ⊥ x 轴于点 C ，

∵ 三角形 AOB 为等边三角形，

∴∠ AOB =60° ，

设点 A （ a ， b ），

则 CO = a ， AO = AB = OB =2 a ，根据勾股定理可得 ∶ AC = b = ，

∵ ，

∴ ， ，解得： a =2 ，

∴ b = ，即点 A (2 ， ) ，

把点 A (2 ， ) 代入 得， k = ，

故选： D ．

【点睛】本题主要考查了反比例函数得图像和性质，等边三角形的性质，熟练的掌握反比例函数的性质和等边三角形的性质是解题的关键．