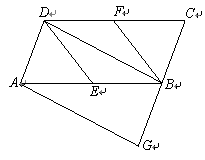
如图,在 中,
,
,
.动点
从点
出发,以
的速度沿边
向终点
匀速运动.以
为一边作
,另一边
与折线
相交于点
,以
为边作菱形
,点
在线段
上.设点
的运动时间为
,菱形
与
重叠部分图形的面积为
.
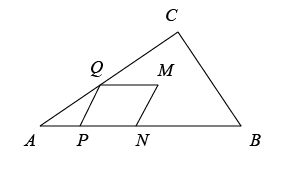
(1) 当点 在边
上时,
的长为
;(用含
的代数式表示)
(2) 当点 落在边
上时,求
的值;
(3) 求 关于
的函数解析式,并写出自变量
的取值范围.
答案
(1)2 x
(2)1
(3)
【分析】( 1 )先证明 ∠ A =∠ AQP =30° ,即 AP = PQ ,根据题意有 AP =2 x ,即 PQ =2 x ;
( 2 )当 M 点在 BC 上, Q 点在 AC 上,在( 1 )中已求得 AP = PQ =2 x ,再证明 △ MNB 是等边三角形,即有 BN = MN ,根据 AB =6 x =6cm ,即有 x =1 ( s );
( 3 )分类讨论:当 时,此时菱形 PQMN 在 △ ABC 的内部,此时菱形 PQMN 与 △ ABC 重叠的面积即是菱形 PQMN 的面积,过 Q 点作 QG ⊥ AB 于 G 点,求出菱形的面积即可;当 x > 1 ,且 Q 点在线段 AC 上时,过 Q 点作 QG ⊥ AB 于 G 点,设 QM 交 BC 于 F 点, MN 交 BC 于 E 点,过 M 点作 NH ⊥ EF 于 H 点,先证明 △ ENB 是等边三角形、 △ MEF 是等边三角形,重叠部分是菱形 PQMN 的面积减去等边 △ MEF 的面积,求出菱形 PQMN 的面积和等边 △ MEF 的面积即可,此时需要求出当 Q 点在 C 点时的临界条件;当
时,此时 Q 点在线段 BC 上,此时 N 点始终与 B 点重合,过 Q 点作 QG ⊥ AB 于 G 点,重叠部分的面积就是 △ PBQ 的面积,求出等边 △ PBQ 的面积即可.
【详解】( 1 )当 Q 点在 AC 上时,
∵∠ A =30° , ∠ APQ =120° ,
∴∠ AQP =30° ,
∴∠ A =∠ AQP ,
∴ AP = PQ ,
∵ 运动速度为每秒 2cm ,运动时间为 x 秒,
∴ AP =2 x ,
∴ PQ =2 x ;
( 2 )当 M 点在 BC 上, Q 点在 AC 上,如图,
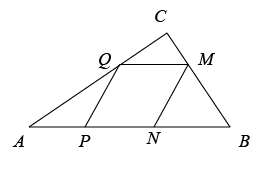
在( 1 )中已求得 AP = PQ =2 x ,
∵ 四边形 QPMN 是菱形,
∴ PQ = PN = MN =2 x , ,
∵∠ APQ =120° ,
∴∠ QPB =60° ,
∵ ,
∴∠ MNB =∠ QPB =60° ,
∵ 在 Rt △ ABC 中, ∠ C =90° , ∠ A =30° ,
∴∠ B =60° ,
∴△ MNB 是等边三角形,
∴ BN = MN ,
∴ AB = AP + PN + BN =2 x ×3=6 x =6cm ,
∴ x =1 ( s );
( 3 )当 P 点运动到 B 点时,用时 6÷2=3 ( s ),
即 x 的取值范围为: ,
当 M 点刚好在 BC 上时,
在( 2 )中已求得此时 x =1 ,
分情况讨论,
即当 时,此时菱形 PQMN 在 △ ABC 的内部,
∴ 此时菱形 PQMN 与 △ ABC 重叠的面积即是菱形 PQMN 的面积,
过 Q 点作 QG ⊥ AB 于 G 点,如图,
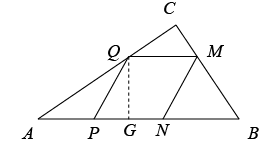
∵∠ APQ =120° ,
∴∠ QPN =60° ,即菱形 PQMN 的内角 ∠ QPN =∠ QMN =60° ,
∴ QG = PQ ×sin∠ QPN =2 x ×sin60°= ,
∴ 重叠的面积等于菱形 PQMN 的面积为,即为: ;
当 x > 1 ,且 Q 点在线段 AC 上时,
过 Q 点作 QG ⊥ AB 于 G 点,设 QM 交 BC 于 F 点, MN 交 BC 于 E 点,过 M 点作 NH ⊥ EF 于 H 点,如图,
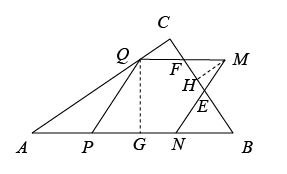
∵ ,
∴∠ MNB =∠ QPN =60 ,
∵∠ B =60° ,
∴△ ENB 是等边三角形,
同理可证明 △ MEF 是等边三角形
∴ BN = NE , ∠ MEF =60° , ME = EF ,
∵ AP = PQ = PN = MN =2 x , AB =6 ,
∴ BN =6- AN =6-4 x ,
∴ ME = MN - NE =2 x - BN =6 x -6 ,
∵ MH ⊥ EF ,
∴ MH = ME ×sin∠ MEH =(6 x -6)×sin60°= ,
∴△ MEF 的面积为: ,
QG = PQ ×sin∠ QPN =2 x ×sin60°= ,
∵ 菱形 PQMN 的面积为 ,
∴ 重叠部分的面积为 ,
当 Q 点与 C 点重合时,可知此时 N 点与 B 点重合,如图,
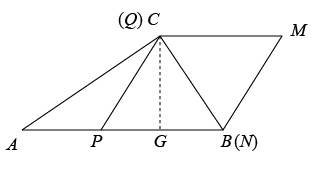
∵∠ CPB =∠ CBA =60° ,
∴△ PBC 是等边三角形,
∴ PC = PB ,
∵ AP = PQ =2 x ,
∴ AP = PB =2 x ,
∴ AB = AP + PB =4 x =6 ,
则 x = ,
即此时重合部分的面积为: ,
;
当 时,此时 Q 点在线段 BC 上,此时 N 点始终与 B 点重合,过 Q 点作 QG ⊥ AB 于 G 点,如图,
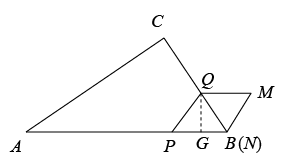
∵ AP =2 x ,
∴ PB = AB - AP =6-2 x ,
∵∠ QPB =∠ ABC =60° ,
∴△ PQB 是等边三角形,
∴ PQ = PB ,同时印证菱形 PQMN 的顶点 N 始终与 B 点重合,
∴ QG = PQ ×sin∠ QPN =(6-2 x )×sin60°= ,
∴ ,
∴ 此时重叠部分的面积 ,
综上所述: .
【点睛】本题考查了一次函数的应用、菱形的性质、等边三角形的判定与性质、等腰三角形的判定与性质、解直角三角形等知识,理清运动过程中 Q 点的位置以及菱形 PQMN 的位置是解答本题的关键.解答本题需要注意分类讨论的思想.