【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
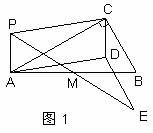
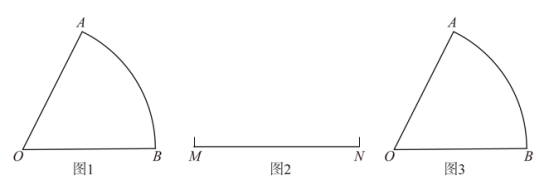
【初步尝试】如图 1 ,已知扇形 ,请你用圆规和无刻度的直尺过圆心
作一条直线,使扇形的面积被这条直线平分;
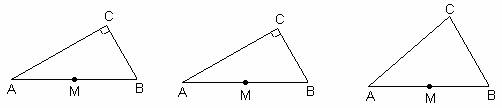
【问题联想】如图 2 ,已知线段 ,请你用圆规和无刻度的直尺作一个以
为斜边的等腰直角三角形
;
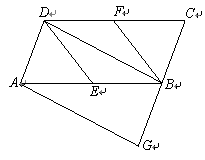
【问题再解】如图 3 ,已知扇形 ,请你用圆规和无刻度的直尺作一条以点
为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
答案
见解析
【分析】【初步尝试】如图 1 ,作 ∠ AOB 的角平分线所在直线即为所求;
【问题联想】如图 2 ,先作 MN 的线段垂直平分线交 MN 于点 O ,再以 O 为圆心 MO 为半径作圆,与垂直平分线的交点即为等腰直角三角形的顶点;
【问题再解】如图 3 先作 OB 的线段垂直平分线交 OB 于点 N ,再以 N 为圆心 NO 为半径作圆 , 与垂直平分线的交点为 M ,然后以 O 为圆心, OM 为半径作圆与扇形 所交的圆弧即为所求.
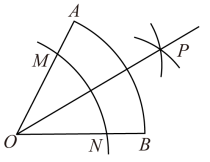
【详解】【初步尝试】如图所示,作 ∠ AOB 的角平分线所在直线 OP 即为所求;
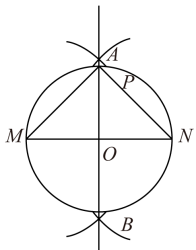
【问题联想】如图,先作 MN 的线段垂直平分线交 MN 于点 O ,再以 O 为圆心 MO 为半径作圆,与垂直平分线的交点即为等腰直角三角形的顶点;
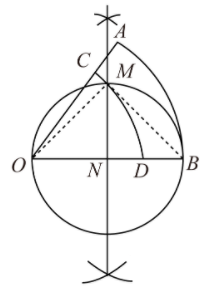
【问题再解】如图,先作 OB 的线段垂直平分线交 OB 于点 N ,再以 N 为圆心 NO 为半径作圆 , 与垂直平分线的交点为 M ,然后以 O 为圆心, OM 为半径作圆与扇形 所交的圆弧 CD 即为所求.
【点睛】本题考查了尺规作图,角平分线的性质,线段垂直平分线的性质,扇形的面积等知识,解决此类题目的关键是熟悉基本几何图形的性质,掌握基本作图方法.