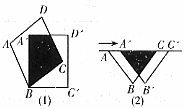
在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图( 1 ),在菱形 中,
为锐角,
为
中点,连接
,将菱形
沿
折叠,得到四边形
,点
的对应点为点
,点
的对应点为点
.
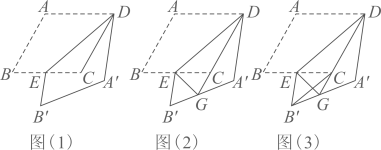
(1) 【观察发现】 与
的位置关系是 ______ ;
(2) 【思考表达】连接 ,判断
与
是否相等,并说明理由;
(3) 如图( 2 ),延长 交
于点
,连接
,请探究
的度数,并说明理由;
(4) 【综合运用】如图( 3 ),当 时,连接
,延长
交
于点
,连接
,请写出
、
、
之间的数量关系,并说明理由.
答案
(1) ;
(2) ,理由见解析;
(3) ,理由见解析;
(4) ,理由见解析.
【分析】( 1 )利用菱形的性质和翻折变换的性质判断即可;
( 2 )连接 ,
,由
可知点 B 、
、 C 在以
为直径 , E 为圆心的圆上,则
,由翻折变换的性质可得
,证明
,可得结论;
( 3 )连接 ,
,
,延长
至点 H ,求出
,
,可得
,然后证明
,可得
,进而得到
即可解决问题.
( 4 )延长 交
的延长线于点
,过点
作
交
的延长线于点
,设
,
,解直角三角形求出
,
,利用勾股定理求出
,然后根据相似三角形的判定和性质及平行线分线段成比例求出
,
,再根据勾股定理列式即可得出结论.
【详解】( 1 )解: ∵ 在菱形 中,
,
∴ 由翻折的性质可知, ,
故答案为: ;
( 2 )解: ,
理由:如图,连接 ,
,
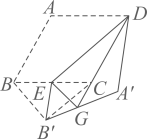
∵ 为
中点,
∴ ,
∴ 点 B 、 、 C 在以
为直径 , E 为圆心的圆上,
∴ ,
∴ ,
由翻折变换的性质可知 ,
∴ ,
∴ ;
( 3 )解:结论: ;
理由:如图,连接 ,
,
,延长
至点 H ,
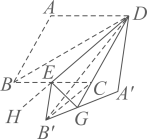
由翻折的性质可知 ,
设 ,
,
∵ 四边形 是菱形,
∴ ,
,
∴ ,
∴ ,
∴ ,
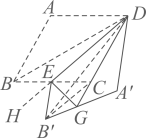
∵ ,点 B 、
、 C 在以
为直径 , E 为圆心的圆上,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ;
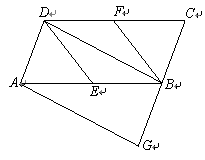
( 4 )解:结论: ,
理由:如图,延长 交
的延长线于点
,过点
作
交
的延长线于点
,
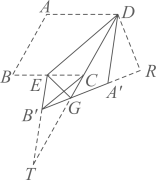
设 ,
,
∵ ,
∴ ,
∴ ,
∴ ,
,
在 中,则有
,
∴ ,
∴ ,
,
∵ ,
∴ ,
∴ ,
∴
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ .
【点睛】本题属于四边形综合题,考查了菱形的性质,翻折变换,圆周角定理,勾股定理,解直角三角形,相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会利用参数解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.