在 △ ABC 中， AB ＝ AC ， ∠ BAC ＝ 90° ， AD 是 △ ABC 的角平分线．
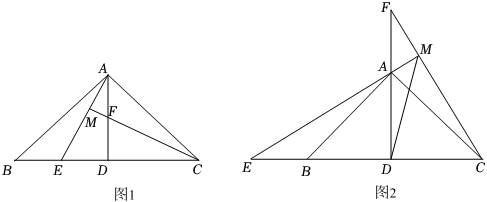
(1) 如图 1 ，点 E 、 F 分别是线段 BD 、 AD 上的点，且 DE ＝ DF ， AE 与 CF 的延长线交于点 M ，则 AE 与 CF 的数量关系是 ，位置关系是 ；
(2) 如图 2 ，点 E 、 F 分别在 DB 和 DA 的延长线上，且 DE ＝ DF ， EA 的延长线交 CF 于点 M ．
① （ 1 ）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；
② 连接 DM ，求 ∠ EMD 的度数；
③ 若 DM ＝ 6 ， ED ＝ 12 ，求 EM 的长．
答案
(1) AE ＝ CF ， AE ⊥ CF
(2)① 成立，理由见解析； ②45° ； ③6+6
【分析】（ 1 ）证明 △ ADE ≌△ CDF （ SAS ），由全等三角形的性质得出 AE ＝ CF ， ∠ DAE ＝ ∠ DCF ，由直角三角形的性质证出 ∠ EMC ＝ 90° ，则可得出结论；
（ 2 ） ① 同（ 1 ）可证 △ ADE ≌△ CDF （ SAS ），由全等三角形的性质得出 AE ＝ CF ， ∠ E ＝ ∠ F ，则可得出结论；
② 过点 D 作 DG ⊥ AE 于点 G ， DH ⊥ CF 于点 H ，证明 △ DEG ≌△ DFH （ AAS ），由全等三角形的性质得出 DG ＝ DH ，由角平分线的性质可得出答案；
③ 由等腰直角三角形的性质求出 GM 的长，由勾股定理求出 EG 的长，则可得出答案．
（ 1 ） ∵ AB ＝ AC ， ∠ BAC ＝ 90° ， AD 是 △ ABC 的角平分线， ∴ AD ＝ BD ＝ CD ， AD ⊥ BC ， ∴∠ ADE ＝ ∠ CDF ＝ 90° ，又 ∵ DE ＝ DF ， ∴△ ADE ≌△ CDF （ SAS ）， ∴ AE ＝ CF ， ∠ DAE ＝ ∠ DCF ， ∵∠ DAE +∠ DEA ＝ 90° ， ∴∠ DCF +∠ DEA ＝ 90° ， ∴∠ EMC ＝ 90° ， ∴ AE ⊥ CF ．故答案为： AE ＝ CF ， AE ⊥ CF ；
（ 2 ） ① （ 1 ）中的结论还成立，理由：同（ 1 ）可证 △ ADE ≌△ CDF （ SAS ）， ∴ AE ＝ CF ， ∠ E ＝ ∠ F ， ∵∠ F +∠ ECF ＝ 90° ， ∴∠ E +∠ ECF ＝ 90° ， ∴∠ EMC ＝ 90° ， ∴ AE ⊥ CF ； ② 过点 D 作 DG ⊥ AE 于点 G ， DH ⊥ CF 于点 H ，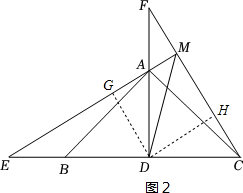 
∵∠ E ＝ ∠ F ， ∠ DGE ＝ ∠ DHF ＝ 90° ， DE ＝ DF ， ∴△ DEG ≌△ DFH （ AAS ）， ∴ DG ＝ DH ，又 ∵ DG ⊥ AE ， DH ⊥ CF ， ∴ DM 平分 ∠ EMC ，又 ∵∠ EMC ＝ 90° ， ∴∠ EMD ＝ ∠ EMC ＝ 45° ； ③∵∠ EMD ＝ 45° ， ∠ DGM ＝ 90° ， ∴∠ DMG ＝ ∠ GDM ， ∴ DG ＝ GM ，又 ∵ DM
∴ DG ＝ GM ＝ 6 ， ∵ DE ＝ 12 ， ∴ EG ＝
∴ EM ＝ GM + EG ＝ 6+6
．
【点睛】本题是三角形综合题，考查了等腰直角三角形的性质，角平分线的性质，全等三角形的判定与性质，勾股定理，熟练掌握全等三角形的判定与性质是解题的关键．
