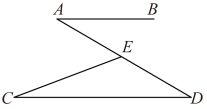
如图，已知 ，点 E 在线段 AD 上（不与点 A ，点 D 重合），连接 CE ．若 ∠ C ＝ 20° ， ∠ AEC ＝ 50° ，则 ∠ A ＝（ ）

A ． 10° B ． 20° C ． 30° D ． 40°

答案

C

【分析】根据三角形外角的性质、平行线的性质进行求解即可；

【详解】解： ∵∠ C +∠ D ＝ ∠ AEC ，

∴∠ D =∠ AEC -∠ C ＝ 50°-20°=30° ，

∵ ，

∴∠ A ＝ ∠ D= 30° ，

故选： C ．

【点睛】本题主要考查三角形外角的性质、平行线的性质，掌握相关性质并灵活应用是解题的关键．