回顾:用数学的思维思考
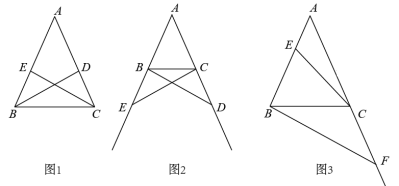
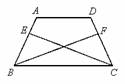
(1) 如图 1 ,在 △ ABC 中, AB = AC .
① BD , CE 是 △ ABC 的角平分线.求证: BD = CE .
② 点 D , E 分别是边 AC , AB 的中点,连接 BD , CE .求证: BD = CE .
(从 ①② 两题中选择一题加以证明)
(2) 猜想:用数学的眼光观察
经过做题反思,小明同学认为:在 △ ABC 中, AB = AC , D 为边 AC 上一动点(不与点 A , C 重合).对于点 D 在边 AC 上的任意位置,在另一边 AB 上总能找到一个与其对应的点 E ,使得 BD = CE .进而提出问题:若点 D , E 分别运动到边 AC , AB 的延长线上, BD 与 CE 还相等吗?请解决下面的问题:
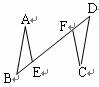
如图 2 ,在 △ ABC 中, AB = AC ,点 D , E 分别在边 AC , AB 的延长线上,请添加一个条件(不再添加新的字母),使得 BD = CE ,并证明.
(3) 探究:用数学的语言表达
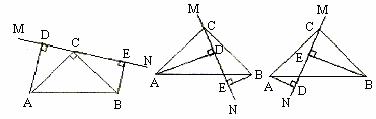
如图 3 ,在 △ ABC 中, AB = AC = 2 , ∠ A = 36° , E 为边 AB 上任意一点(不与点 A , B 重合), F 为边 AC 延长线上一点.判断 BF 与 CE 能否相等.若能,求 CF 的取值范围;若不能,说明理由.
答案
(1) 见解析
(2) 添加条件 CD = BE ,见解析
(3) 能, 0 < CF <
【分析】( 1 ) ① 利用 ASA 证明 △ ABD ≌△ ACE .
② 利用 SAS 证明 △ ABD ≌△ ACE .
( 2 )添加条件 CD = BE ,证明 AC + CD = AB + BE ,从而利用 SAS 证明 △ ABD ≌△ ACE .
( 3 )在 AC 上取一点 D ,使得 BD = CE ,根据 BF = CE ,得到 BD = BF ,当 BD = BF = BA 时,可证 △ CBF ∽△ BAF ,运用相似性质,求得 CF 的长即可.
【详解】( 1 ) ① 如图 1 , ∵ AB = AC ,
∴∠ ABC =∠ ACB ,
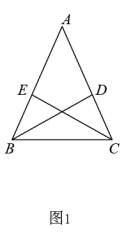
∵ BD , CE 是 △ ABC 的角平分线,
∴∠ ABD = ∠ ABC , ∠ ACE =
∠ ACB ,
∴∠ ABD =∠ ACE ,
∵ AB = AC , ∠ A =∠ A ,
∴△ ABD ≌△ ACE ,
∴ BD = CE .
② 如图 1 , ∵ AB = AC ,点 D , E 分别是边 AC , AB 的中点,
∴ AE = AD ,
∵ AB = AC , ∠ A =∠ A ,
∴△ ABD ≌△ ACE ,
∴ BD = CE .
( 2 )添加条件 CD = BE ,证明如下:
∵ AB = AC , CD = BE ,
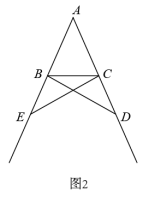
∴ AC + CD = AB + BE ,
∴ AD = AE ,
∵ AB = AC , ∠ A =∠ A ,
∴△ ABD ≌△ ACE ,
∴ BD = CE .
( 3 )能
在 AC 上取一点 D ,使得 BD = CE ,根据 BF = CE ,得到 BD = BF ,
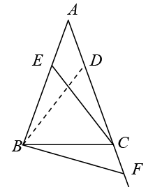
当 BD = BF = BA 时, E 与 A 重合,
∵∠ A = 36° , AB = AC ,
∴∠ ABC =∠ ACB =72° , ∠ A =∠ BFA =36° ,
∴∠ ABF =∠ BCF =108° , ∠ BFC =∠ AFB ,
∴ △ CBF ∽△ BAF ,
∴ ,
∵ AB = AC = 2= BF , 设 CF = x ,
∴ ,
整理,得 ,
解得 x = , x =
(舍去),
故 CF = x = ,
∴0 < CF < .
【点睛】本题考查了等腰三角形的性质,三角形全等的判定和性质,三角形相似的判定和性质,一元二次方程的解法,熟练掌握等腰三角形的性质,三角形全等的判定,三角形相似的判定性质是解题的关键.