探索发现

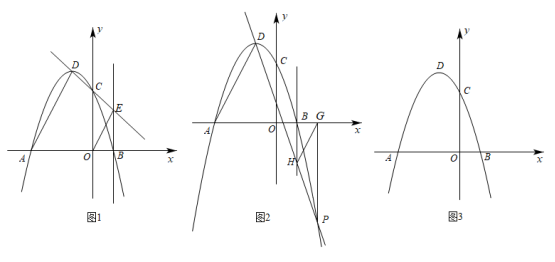
(1) 在平面直角坐标系中，抛物线 y ＝ ax ² + bx +3 （ a ≠ 0 ）与 x 轴交于点 A （﹣ 3 ， 0 ）， B （ 1 ， 0 ），与 y 轴交于点 C ，顶点为点 D ，连接 AD ．

① 如图 1 ，直线 DC 交直线 x ＝ 1 于点 E ，连接 OE ．求证： AD ∥ OE ；

② 如图 2 ，点 P （ 2 ，﹣ 5 ）为抛物线 y ＝ ax ² + bx +3 （ a ≠ 0 ）上一点，过点 P 作 PG ⊥ x 轴，垂足为点 G ．直线 DP 交直线 x ＝ 1 于点 H ，连接 HG ．求证： AD ∥ HG ；

(2) 通过上述两种特殊情况的证明，你是否有所发现？请仿照（ 1 ）写出你的猜想，并在图 3 上画出草图．在平面直角坐标系中，抛物线 y ＝ ax ² + bx +3 （ a ≠ 0 ）与 x 轴交于点 A （﹣ 3 ， 0 ）， B （ 1 ， 0 ），顶点为点 D ．点 M 为该抛物线上一动点（不与点 A ， B ， D 重合）， _______．

答案

(1)① 见解析； ② 见解析

(2) 猜想：作 MN ⊥ x 轴于 N ，直线 DM 交直线 x =1 于 Q ，则 QN ∥ AD ，证明见解析

【分析】（ 1 ） ① 将点 A 和 B 点的坐标代入抛物线的解析式，从而求得 a ， b 的值，从而得出抛物线的解析式，从而得出点 D 和点 C 坐标，进而求得 E 点坐标和 AD 的解析式，再求出 OE 的解析式，从而得出结论；

② 方法 ① 求得 GH 的解析式，进而得出结论；

（ 2 ）作 MN ⊥ x 轴于 N ，直线 DM 交直线 x =1 于 Q ，则 QN ∥ AD ，方法同 ① 相同可推出结论．

【详解】（ 1 ）解：（ 1 ） ① 由题意得，

，

∴ ，

∴ y =- x ² -2 x +3=- （ x +1 ） ² +4 ，

∴ D （ -1 ， 4 ）， C （ 0 ， 3 ），

设直线 CD 的解析式为： y = mx + n ，

∴ ，

∴ ，

∴ y =- x +3 ，

∴ 当 x =1 时， y =-1+3=2 ，

∴ E （ 1 ， 2 ），

∴ 直线 OE 的解析式为： y =2 x ，

设直线 AD 的解析式为 y = cx + d ，

∴ ，

∴ ，

∴ y =2 x +6 ，

∴ OE ∥ AD ；

② 设直线 PD 的解析式为： y = ex + f ，

∴ ，

∴ ，

∴ y =-3 x +1 ，

∴ 当 x =1 时， y =-3×1+1=-2 ，

∴ H （ 1 ， -2 ），

设直线 GH 的解析式为： y = gx + h ，

∴ ，

∴ ，

∴ y =2 x -4 ，

∴ AD ∥ HG ；

（ 2 ）猜想：作 MN ⊥ x 轴于 N ，直线 DM 交直线 x =1 于 Q ，连接 NQ ，则 QN ∥ AD ，如图，

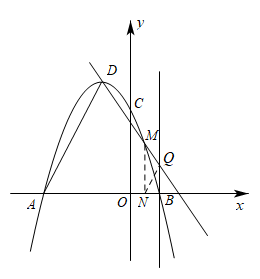
证明如下：

设 M （ m ， - m ² -2 m +3 ），

设直线 DM 的解析式为 y = px + q ，

∴ ，

∴ ，

∴ y =- （ m +1 ） x + （ - m +3 ），

∴ 当 x =1 时， y =- m -1- m +3=-2 m +2 ，

∴ Q （ 1 ， -2 m +2 ），

设直线 NQ 的解析式为： y = ix + j ，

∴ ，

∴ ，

∴ y =2 x -2 m ，

∴ QN ∥ AD ．

【点睛】本题考查了求二次函数的解析式，求一次函数解析式，一次函数图象性质等知识，解决问题的关键是掌握一次函数平移的性质．

．