如图 :
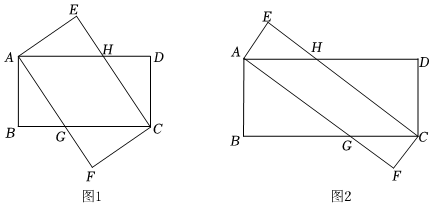
(1) 将两张长为 8 ,宽为 4 的矩形纸片如图 1 叠放.
① 判断四边形 AGCH 的形状,并说明理由;
② 求四边形 AGCH 的面积.
(2) 如图 2 ,在矩形 ABCD 和矩形 AFCE 中, AB = 2 , BC = 7 , CF =
,求四边形 AGCH 的面积.
答案
(1)① 菱形,理由见解析; ②20
(2)
【分析】( 1 ) ① 根据邻边相等的平行四边形是菱形证明即可; ② 设 AH = CG = x ,利用勾股定理构建方程即可解决问题;
( 2 )两个矩形的对角线相等,可得出 EC 的长,设 AH = CG = x ,利用勾股定理以及边长之间的关系可得出 x 的值,进而可求出面积.
【详解】( 1 ) ①∵ 四边形 ABCD ,四边形 AECF 都是矩形
∴
∴ 四边形 AHCG 为平行四边形
∵
∴
∴
∴ 四边形 AHCG 为菱形;
② 设 AH = CG = x ,则 DH = AD - AH =8- x
在 中
即
解得
∴ 四边形 AHCG 的面积为 ;
( 2 )由图可得矩形 ABCD 和矩形 AFCE 对角线相等
∴
∴
设 AH = CG = x 则 HD =7- x
在 中,
在 中,
∵ EC = EH + CH =8
∴ x =3
∴ 四边形 AGCH 的面积为 .
【点睛】本题考查了矩形的性质,菱形的判定和性质,解直角三角形等知识,解题的关键是学会利用参数构建方程解决问题.

 。
。