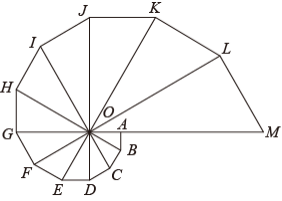
由 12 个有公共顶点 O 的直角三角形拼成如图所示的图形， ∠ AOB ＝ ∠ BOC ＝ ∠ COD ＝ …＝∠ LOM ＝ 30 °．若 S △ AOB ＝ 1 ，则图中与 △ AOB 位似的三角形的面积为 ( )

A ． （ ） ³ B ． （ ） ⁷ C ． （ ） ⁶ D ． （ ） ⁶

答案

C

【分析】根据题意得出 A 、 O 、 G 在同一直线上， B 、 O 、 H 在同一直线上，确定与 △ AOB 位似的三角形为 △ GOH ，利用锐角三角函数找出相应规律得出 OG = ，再由相似三角形的性质求解即可．

【详解】解： ∵∠ AOB ＝ ∠ BOC ＝ ∠ COD ＝ … ＝ ∠ LOM ＝ 30°

∴∠ AOG ＝ 180° ， ∠ BOH ＝ 180° ，

∴ A 、 O 、 G 在同一直线上， B 、 O 、 H 在同一直线上，

∴ 与 △ AOB 位似的三角形为 △ GOH ，

设 OA = x ，

则 OB = ，

∴ OC = ，

∴ OD = ，

…

∴ OG = ，

∴ ，

∴ ，

∵ ，

∴ ，

故选： C ．

【点睛】题目主要考查利用锐角三角函数解三角形，找规律问题，相似三角形的性质等，理解题意，找出相应边的比值规律是解题关键．