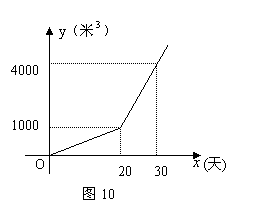
如图，在方格纸中，点 P ， Q ， M 的坐标分别记为（ 0 ， 2 ），（ 3 ， 0 ），（ 1 ， 4 ）．若 MN ∥ PQ ，则点 N 的坐标可能是 ( )

A ． （ 2 ， 3 ） B ． （ 3 ， 3 ） C ． （ 4 ， 2 ） D ． （ 5 ， 1 ）

答案

C

【分析】根据 P ， Q 的坐标求得直线解析式，进而求得过点 的解析式，即可求解．

【详解】解： ∵ P ， Q 的坐标分别为（ 0 ， 2 ），（ 3 ， 0 ），设直线 的解析式为 ，

则 ，

解得 ，

直线 的解析式为 ，

MN ∥ PQ ，

设 的解析式为 ， ，

则 ，

解得 ，

的解析式为 ，

当 时， ，

当 时， ，

当 时， ，

当 时， ，

故选 C

【点睛】本题考查了求一次函数解析式，一次函数平移问题，掌握以上知识是解题的关键．