某城市几条道路的位置关系如图所示，道路 ，道路 AB 与 AE 的夹角 ∠ BAE ＝ 50° ．城市规划部门想新修一条道路 CE ，要求 CF ＝ EF ，则 ∠ E 的度数为（ ）

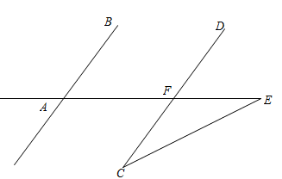
A ． 23° B ． 25° C ． 27° D ． 30°

答案

B

【分析】先根据平行线的性质，由 得到 ∠ BAE =∠ DFE =50° ，然后根据三角形外角性质计算 ∠ E 的度数．

【详解】解： ∵ ， ∠ BAE ＝ 50° ，

∴∠ BAE =∠ DFE =50° ，

∵ CF ＝ EF ，

∴∠ C =∠ E ，

∵∠ DFE =∠ C +∠ E =50° ，

∴∠ E =25° ．

故选： B ．

【点睛】本题考查了平行线的性质，等腰三角形的性质，以及三角形的外角性质，熟练掌握平行线的性质是解题的关键．