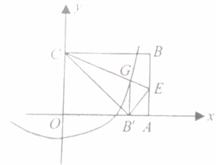
如图，已知直线 y ＝ x +4 与 x 轴交于点 A ，与 y 轴交于点 C ，抛物线 y ＝ ax ² + bx + c 经过 A ， C 两点，且与 x 轴的另一个交点为 B ，对称轴为直线 x ＝﹣ 1 ．

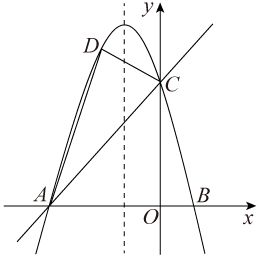
(1) 求抛物线的表达式；

(2) D 是第二象限内抛物线上的动点，设点 D 的横坐标为 m ，求四边形 ABCD 面积 S 的最大值及此时 D 点的坐标；

(3) 若点 P 在抛物线对称轴上，是否存在点 P ， Q ，使以点 A ， C ， P ， Q 为顶点的四边形是以 AC 为对角线的菱形？若存在，请求出 P ， Q 两点的坐标；若不存在，请说明理由．

答案

(1) y ＝﹣ x ² ﹣ x +4

(2)S _最大 ＝ ， D （﹣ ， 5 ）

(3) 存在， Q （﹣ 2 ， ）

【分析】（ 1 ）先求得 A ， C ， B 三点的坐标，将抛物线设为交点式，进一步求得结果；

（ 2 ）作 DF ⊥ AB 于 F ，交 AC 于 E ，根据点 D 和点 E 坐标可表示出 DE 的长，进而表示出三角形 ADC 的面积，进而表示出 S 的函数关系式，进一步求得结果；

（ 3 ）根据菱形性质可得 PA ＝ PC ，进而求得点 P 的坐标，根据菱形性质，进一步求得点 Q 坐标．

【详解】（ 1 ）解：当 x ＝ 0 时， y ＝ 4 ，

∴ C （ 0 ， 4 ），

当 y ＝ 0 时， x +4 ＝ 0 ，

∴ x ＝﹣ 3 ，

∴ A （﹣ 3 ， 0 ），

∵ 对称轴为直线 x ＝﹣ 1 ，

∴ B （ 1 ， 0 ），

∴ 设抛物线的表达式： y ＝ a （ x ﹣ 1 ） • （ x +3 ），

∴4 ＝﹣ 3 a ，

∴ a ＝﹣ ，

∴ 抛物线的表达式为： y ＝﹣ （ x ﹣ 1 ） • （ x +3 ）＝﹣ x ² ﹣ x +4 ；

（ 2 ）如图 1 ，

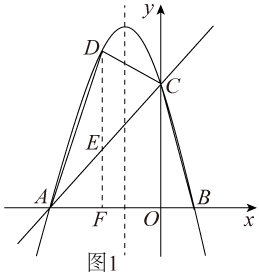
作 DF ⊥ AB 于 F ，交 AC 于 E ，

∴ D （ m ，﹣ ﹣ m +4 ）， E （ m ， m +4 ），

∴ DE ＝﹣ ﹣ m +4 ﹣（ m +4 ）＝﹣ m ² ﹣ 4 m ，

∴ S _△ ADC ＝ OA ＝ • （﹣ m ² ﹣ 4 m ）＝﹣ 2 m ² ﹣ 6 m ，

∵ S _△ ABC ＝ ＝ ＝ 8 ，

∴ S ＝﹣ 2 m ² ﹣ 6 m +8 ＝﹣ 2 （ m + ） ² + ，

∴ 当 m ＝﹣ 时， S _最大 ＝ ，

当 m ＝﹣ 时， y ＝﹣ ＝ 5 ，

∴ D （﹣ ， 5 ）；

（ 3 ）设 P （﹣ 1 ， n ），

∵ 以 A ， C ， P ， Q 为顶点的四边形是以 AC 为对角线的菱形，

∴ PA ＝ PC ，

即： PA ² ＝ PC ² ，

∴ （﹣ 1+3 ） ² + n ² ＝ 1+ （ n ﹣ 4 ） ² ，

∴ n ＝ ，

∴ P （﹣ 1 ， ），

∵ xP + xQ ＝ xA + xC ， yP + yQ ＝ yA + yC

∴ xQ ＝﹣ 3 ﹣（﹣ 1 ）＝﹣ 2 ， yQ ＝ 4 ﹣ ＝ ，

∴ Q （﹣ 2 ， ）．

【点睛】本题考查了二次函数及其图象性质，勾股定理，菱形性质等知识，解决问题的关键是熟练掌握相关二次函数和菱形性质