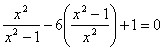已知关于 x 的一元二次方程 有两个不等实数根 ， ．

(1) 求 k 的取值范围；

(2) 若 ，求 k 的值．

答案

(1)

(2)2

【分析】（ 1 ）利用一元二次方程根的判别式大于 0 建立不等式，解不等式即可得；

（ 2 ）先利用一元二次方程的根与系数的关系可得 ，再结合（ 1 ）的结论即可得．

【详解】（ 1 ）解： 关于 的一元二次方程 有两个不等实数根，

此方程根的判别式 ，

解得 ．

（ 2 ）解：由题意得： ，

解得 或 ，

由（ 1 ）已得： ，

则 的值为 2 ．

【点睛】本题考查了一元二次方程根的判别式、以及根与系数的关系，熟练掌握一元二次方程的相关知识是解题关键．