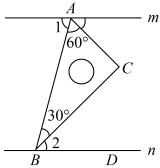
已知直线 m∥n ，将一块含 30° 角的直角三角板 ABC （ ∠ ABC ＝ 30° ， ∠ BAC ＝ 60° ）按如图方式放置，点 A ， B 分别落在直线 m ， n 上．若 ∠1 ＝ 70° ．则 ∠2 的度数为（ ）

A ． 30° B ． 40° C ． 60° D ． 70°

答案

B

【分析】根据平行线的性质求得 ∠ ABD ，再根据角的和差关系求得结果．

【详解】解： ∵ m n ， ∠1=70° ，

∴∠1=∠ ABD =70° ，

∵∠ ABC =30° ，

∴∠2=∠ ABD -∠ ABC =40° ，

故选： B ．

【点睛】本题主要考查了平行线的性质，关键是熟练掌握平行线的性质．