已知菱形 中,
是边
的中点,
是边
上一点.
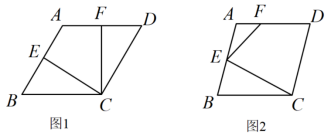
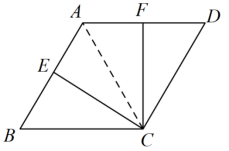
(1) 如图 1 ,连接 ,
.
,
.
① 求证: ;
② 若 ,求
的长;
(2) 如图 2 ,连接 ,
.若
,
,求
的长.
答案
(1)① 见解析; ②
(2)
【分析】( 1 ) ① 根据 可证得:
,即可得出结论;
② 连接 ,可证得
是等边三角形,即可求出
;
( 2 )延长 交
的延长线于点
,根据
可证得
,可得出
,
,
,则
,即可证得
,即可得出
的长.
【详解】( 1 )( 1 ) ①∵ ,
,
∴ ,
∵ 四边形 是菱形,
∴ ,
,
∴ ,
∴ .
② 如图,连接 .
∵ 是边
的中点,
,
∴ ,
又由菱形 ,得
,
∴ 是等边三角形,
∴ ,
在 中,
,
∴ ,
∴ .
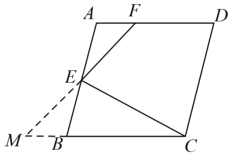
( 2 )如图,延长 交
的延长线于点
,
由菱形 ,得
,
,
∴ ,
,
∵ 是边
的中点,
∴ ,
∴ ,
∴ ,
,
∵ ,
,
∴ ,
,
,
∴ ,
∴ ,
∴ ,
,
∴ ,而
为公共角 .
∴ ,
∴ ,
又 ∵ ,
∴ .
【点睛】本题考查了菱形的性质,等边三角形的性质与判定,锐角三角函数求线段长度,全等三角形的性质和判定,相似三角形的性质与判定,掌握以上知识点并灵活运用是解题的关键 .