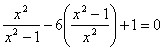阅读材料，解答问题：

材料 1

为了解方程 ，如果我们把 看作一个整体，然后设 ，则原方程可化为 ，经过运算，原方程的解为 ， ．我们把以上这种解决问题的方法通常叫做换元法．

材料 2

已知实数 m ， n 满足 ， ，且 ，显然 m ， n 是方程 的两个不相等的实数根，由韦达定理可知 ， ．

根据上述材料，解决以下问题：

(1) 直接应用：

方程 的解为 _______________________ ；

(2) 间接应用：

已知实数 a ， b 满足： ， 且 ，求 的值；

(3) 拓展应用：

已知实数 x ， y 满足： ， 且 ，求 的值．

答案

(1) ， ， ，

(2) 或

(3)15

【分析】（ 1 ）利用换元法降次解决问题；

（ 2 ）模仿例题解决问题即可；

（ 3 ）令 = a ， - n = b ，则 + a -7=0 ， + b =0 ，再模仿例题解决问题．

【详解】（ 1 ）解：令 y = ，则有 -5 y +6=0 ，

∴ （ y -2 ）（ y -3 ） =0 ，

∴ =2 ， =3 ，

∴ =2 或 3 ，

∴ ， ， ， ，

故答案为： ， ， ， ；

（ 2 ）解： ∵ ，

∴ 或

① 当 时，令 ， ，

∴ 则 ， ，

∴ ， 是方程 的两个不相等的实数根，

∴ ，

此时 ；

② 当 时， ，

此时 ；

综上： 或

（ 3 ）解：令 ， ，则 ， ，

∵ ，

∴ 即 ，

∴ ， 是方程 的两个不相等的实数根，

∴ ，

故 ．

【点睛】本题考查了根与系数的关系，幂的乘方与积的乘方，换元法，解一元二次方程等知识，解题的关键是理解题意，学会模仿例题解决问题．