已知抛物线 ．

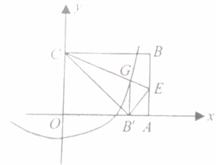
(1) 如图 ① ，若抛物线图象与 轴交于点 ，与 轴交点 ．连接 ．

① 求该抛物线所表示的二次函数表达式；

② 若点 是抛物线上一动点（与点 不重合），过点 作 轴于点 ，与线段 交于点 ．是否存在点 使得点 是线段 的三等分点？若存在，请求出点 的坐标；若不存在，请说明理由．

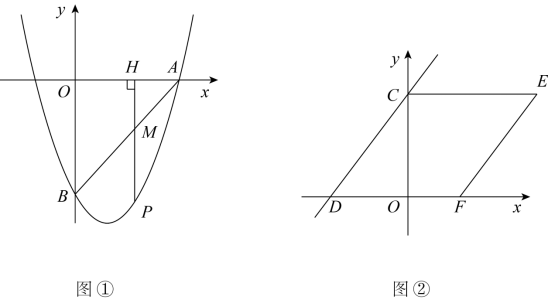
(2) 如图 ② ，直线 与 轴交于点 ，同时与抛物线 交于点 ，以线段 为边作菱形 ，使点 落在 轴的正半轴上，若该抛物线与线段 没有交点，求 的取值范围．

答案

(1)① ， ② 存在，点 P 坐标为 (2 ， -3) 或（ ， - ），理由见解析

(2) b < 或 b >

【分析】（ 1 ） ① 直接用待定系数法求解； ② 先求出直线 AB 的解析式，设点 M ( m ， m -3) 点 P （ m ， m ² -2 m -3 ）若点 是线段 的三等分点，则 或 ，代入求解即可；

（ 2 ）先用待定系数法求出 n 的值，再利用勾股定理求出 CD 的长为 5 ，因为四边形 CDFE 是菱形，由此得出点 E 的坐标．再根据该抛物线与线段 没有交点，分两种情况（ CE 在抛物线内和 CE 在抛物线右侧）进行讨论，求出 b 的取值范围．

【详解】（ 1 ） ① 解：把 ， 代入 ，得

，

解得： ，

∴

② 解：存在，理由如下，

设直线 AB 的解析式为 y = kx + b ，把 ， 代入，得

，

解得 ，

∴ 直线 AB 的解析式为 y = x -3 ，

设点 M ( m ， m -3) 、点 P （ m ， m ² -2 m -3 ）

若点 是线段 的三等分点，

则 或 ，

即 或 ，

解得： m =2 或 m = 或 m =3 ，

经检验， m =3 是原方程的增根，故舍去，

∴ m =2 或 m =

∴ 点 P 坐标为 (2 ， -3) 或（ ， - ）

（ 2 ）解：把点 D （ -3 ， 0 ）代入直线 ，解得 n =4 ，

∴ 直线 ，

当 x =0 时， y =4 ，即点 C （ 0 ， 4 ）

∴ CD = =5 ，

∵ 四边形 CDFE 是菱形，

∴ CE = EF = DF = CD =5 ，

∴ 点 E （ 5 ， 4 ）

∵ 点 在抛物线 上，

∴ （ -3 ） ² -3 b + c =0 ，

∴ c =3 b -9 ，

∴ ，

∵ 该抛物线与线段 没有交点，

分情况讨论

当 CE 在抛物线内时

5 ² +5 b +3 b -9<4

解得： b <

当 CE 在抛物线右侧时，

3 b -9>4

解得： b >

综上所述， b < 或 b >

【点睛】此题考查了二次函数和一次函数以及图形的综合，解题的关键是数形结合和分情况讨论．