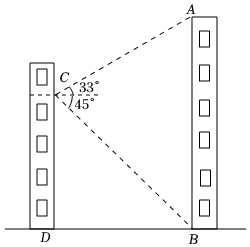
如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼 AB 的高度进行测量，从小敏家阳台 C 测得点 A 的仰角为 33° ，测得点 B 的俯角为 45° ，已知观测点到地面的高度 CD ＝ 36m ，求居民楼 AB 的高度（结果保留整数．参考数据： sin33°≈0.55 ， cos33°≈0.84 ， tan33°≈0.65 ）．

答案

59m

【分析】过点 C 作 CE ⊥ AB 于点 E ，则 ∠ AEC ＝ ∠ BEC ＝ 90° ，先证明四边形 BECD 是矩形， BE ＝ CD ＝ 36m ，在 R t △ BCE 中， ∠ BCE ＝ 45° ， BE ＝ CE ＝ CD ＝ 36m ，在 R t △ ACE 中， ∠ ACE ＝ 33° ， CE ＝ 36m ，求得 AE ≈23.4m ，进而得到居民楼 AB 的高度．

【详解】解：如图，过点 C 作 CE ⊥ AB 于点 E ，则 ∠ AEC ＝ ∠ BEC ＝ 90° ，

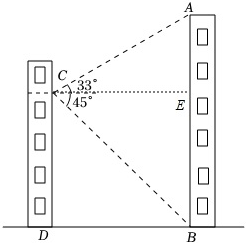
由题意可知 ∠ CDB ＝ ∠ DBE ＝ 90° ，

∴ 四边形 BECD 是矩形，

∴ BE ＝ CD ＝ 36m ，

由题意得， CD ＝ 36m ， ∠ BCE ＝ 45° ， ∠ ACE ＝ 33° ，

在 R t △ BCE 中， ∠ BCE ＝ 45° ，

∴∠ EBC ＝ 90° － ∠ BCE ＝ 45° ，

∴∠ EBC ＝ ∠ BCE ，

∴ BE ＝ CE ＝ CD ＝ 36m ，

在 R t△ ACE 中， ∠ ACE ＝ 33° ， CE ＝ 36m ，

∴ AE ＝ CE tan33°≈23.4m ，

∴ AB ＝ AE ＋ BE ＝ 23.4 ＋ 36 ＝ 59.4≈59 （ m ）．

答：居民楼 AB 的高度约为 59m ．

【点睛】此题考查了解直角三角形的应用中的仰角俯角问题，熟练掌握直角三角形的边角关系是解题的关键．