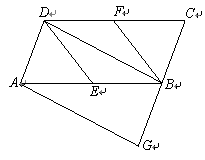
如图,在菱形 ABCD 中, ∠ BAD = 120° , AB = 6 ,连接 BD .
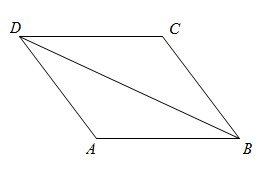
(1) 求 BD 的长;
(2) 点 E 为线段 BD 上一动点(不与点 B , D 重合), 点 F 在边 AD 上,且 BE = DF ,
① 当 CE 丄 AB 时,求四边形 ABEF 的面积;
② 当四边形 ABEF 的面积取得最小值时, CE + CF 的值是否也最小?如果是,求 CE +
CF 的最小值;如果不是,请说明理由.
答案
(1) ;
(2)① 四边形 ABEF 的面积为 ; ② 最小值为 12
【分析】( 1 )证明 △ ABC 是等边三角形,可得 BO = ,即可求解;
( 2 )过点 E 作 AD 的垂线,分别交 AD 和 BC 于点 M , N , 根据菱形的面积可求出 MN = ,设 BE =
,则 EN =
,从而得到 EM = MN - EN =
,再由 BE =
DF ,可得 DF =
,从而得到四边形 ABEF 的面积 s = S △ ABD - S △ DEF
, ① 当 CE ⊥ AB 时,可得点 E 是 △ ABC 重心,从而得到 BE = CE =
BO =
,即可求解; ② 作 CH ⊥ AD 于 H ,可得当点 E 和 F 分别到达点 O 和点 H 位置时, CF 和 CE 分别达到最小值;再由
,可得当
,即 BE =
时, s 达到最小值,从而得到此时点 E 恰好在点 O 的位置,而点 F 也恰好在点 H 位置,即可求解.
【详解】( 1 )解 ∶ 连接 AC ,设 AC 与 BD 的交点为 O ,如图,
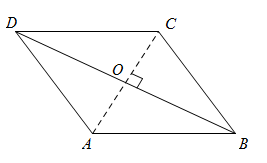
∵ 四边形 ABCD 是菱形,
∴ AC ⊥ BD , OA = OC , AB ∥ CD , AC 平分 ∠ DAB ,
∵∠ BAD = 120° ,
∴∠ CAB =60° ,
∴△ ABC 是等边三角形,
∴ BO = AB ▪sin60°= =
,
∴ BD =2 BO = ;
( 2 )解:如图,过点 E 作 AD 的垂线,分别交 AD 和 BC 于点 M , N ,
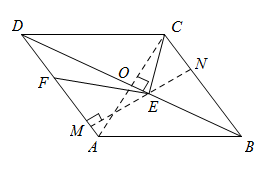
∵△ ABC 是等边三角形,
∴ AC = AB =6 ,
由( 1 )得: BD = ;
菱形 ABCD 中,对角线 BD 平分 ∠ ABC , AB ∥ CD , BC = AB =6 ,
∴ MN ⊥ BC ,
∵∠ BAD =120° ,
∴∠ ABC =60° ,
∴∠ EBN =30° ;
∴ EN = BE
∵ ,
∴ MN = ,
设 BE = ,则 EN =
,
∴ EM = MN - EN = ,
∵ S 菱形 ABCD = AD ▪ MN = ,
∴ S △ ABD = S 菱形 ABCD =
,
∵ BE = DF ,
∴ DF = ,
∴ S △ DEF = DF ▪ EM =
=
,
记四边形 ABEF 的面积为 s ,
∴ s = S △ ABD - S △ DEF = - (
)
,
∵ 点 E 在 BD 上,且不在端点, ∴0< BE < BD ,即 ;
① 当 CE ⊥ AB 时,
∵ OB ⊥ AC ,
∴ 点 E 是 △ ABC 重心,
∴ BE = CE = BO =
,
此时 =
,
∴ 当 CE ⊥ AB 时,四边形 ABEF 的面积为 ;
② 作 CH ⊥ AD 于 H ,如图,
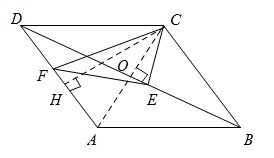
∵ CO ⊥ BD , CH ⊥ AD ,而点 E 和 F 分别在 BD 和 AD 上,
∴ 当点 E 和 F 分别到达点 O 和点 H 位置时, CF 和 CE 分别达到最小值;
在菱形 ABCD 中, AB ∥ CD , AD = CD ,
∵∠ BAD =120° ,
∴∠ ADC =60° ,
∴△ ACD 是等边三角形,
∴ AH = DH =3 ,
∴ CH = ,
∵ ,
∴ 当 ,即 BE =
时, s 达到最小值,
∵ BE = DF ,
∴ DF =3 ,
此时点 E 恰好在点 O 的位置,而点 F 也恰好在点 H 位置,
∴ 当四边形 ABEF 面积取得最小值时, CE 和 CF 也恰好同时达到最小值,
∴ CE + CF 的值达到最小,
其最小值为 CO + CH =
=12 .
【点睛】本题主要考查了菱形的性质,等边三角形的判定和性质,二次函数的性质,三角形的重心,解直角三角形等知识,熟练掌握菱形的性质,等边三角形的判定和性质,二次函数的性质,三角形的重心,解直角三角形等知识是解题的关键.