已知:点 C , D 均在直线 l 的上方, 与
都是直线 l 的垂线段,且
在
的右侧,
,
与
相交于点 O .

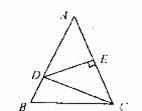
(1) 如图 1 ,若连接 ,则
的形状为 ______ ,
的值为 ______ ;
(2) 若将 沿直线 l 平移,并以
为一边在直线 l 的上方作等边
.
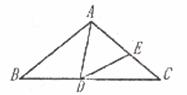
① 如图 2 ,当 与
重合时,连接
,若
,求
的长;
② 如图 3 ,当 时,连接
并延长交直线 l 于点 F ,连接
.求证:
.
答案
(1) 等腰三角形,
(2)① ; ② 见解析
【分析】( 1 )过点 C 作 CH ⊥ BD 于 H ,可得四边形 ABHC 是矩形,即可求得 AC = BH ,进而可判断 △ BCD 的形状, AC 、 BD 都垂直于 l ,可得 △ AOC ∽△ BOD ,根据三角形相似的性质即可求解.
( 2 ) ① 过点 E 作 于点 H , AC , BD 均是直线 l 的垂线段,可得
,根据等边三角形的性质可得
,再利用勾股定理即可求解.
② 连接 ,根据
,得
,即
是等边三角形,把
旋转得
,根据 30° 角所对的直角边等于斜边的一般得到
,则可得
,根据三角形相似的性质即可求证结论.
( 1 )
解:过点 C 作 CH ⊥ BD 于 H ,如图所示:

∵ AC ⊥ l , DB ⊥ l , CH ⊥ BD ,
∴∠ CAB =∠ ABD =∠ CHB =90° ,
∴ 四边形 ABHC 是矩形,
∴ AC = BH ,
又 ∵ BD =2 AC ,
∴ AC = BH = DH ,且 CH ⊥ BD ,
∴ 的形状为等腰三角形,
∵ AC 、 BD 都垂直于 l ,
∴ ,
∴△ AOC ∽△ BOD ,
,即
,
,
故答案为:等腰三角形, .
( 2 )
① 过点 E 作 于点 H ,如图所示:

∵ AC , BD 均是直线 l 的垂线段,
∴ ,
∵ 是等边三角形,且
与
重合,
∴∠ EAD =60° ,
∴ ,
∴ ,
∴ 在 中,
,
,
又 ∵ ,
,
∴ ,
∴ , AE =6
在 中,
,
又由( 1 )知 ,
∴ ,则
,
∴ 在 中,由勾股定理得:
.
② 连接 ,如图 3 所示:

∵ ,
∴ ,
∵ 由( 1 )知 是等腰三角形,
∴ 是等边三角形,
又 ∵ 是等边三角形,
∴ 绕点 D 顺时针旋转
后与
重合,
∴ ,
又 ∵ ,
∴ ,
∴ ,
∴ ,
又 ,
∴ ,
∴ ,
∴ .
【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用,熟练掌握三角形相似的判定及性质和勾股定理的应用,巧妙借助辅助线是解题的关键.