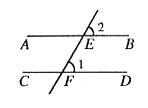
如图，直线 a ， b 被直线 c 所截，且 a b ，若 ∠1 ＝ 60° ，则 ∠2 的度数是（ ）

A ． 70° B ． 60° C ． 50° D ． 40°

答案

B

【分析】根据平行线的性质可以得到 ∠1 ＝ ∠2 ，然后根据 ∠1 的度数，即可得到 ∠2 的度数．

【详解】解： ∵ a ∥ b ，

∴∠1 ＝ ∠2 ，

∵∠1 ＝ 60° ，

∴∠2 ＝ 60° ，

故选： B ．

【点睛】本题考查平行线的性质，解答本题的关键是明确两直线平行，同位角相等．