在 Rt △ ABC 中， AC ＝ BC ，将线段 CA 绕点 C 旋转 α （ 0° ＜ α ＜ 90° ），得到线段 CD ，连接 AD 、 BD ．

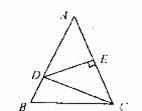
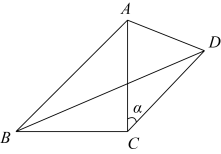
(1) 如图 1 ，将线段 CA 绕点 C 逆时针旋转 α ，则 ∠ ADB 的度数为 ；

(2) 将线段 CA 绕点 C 顺时针旋转 α 时

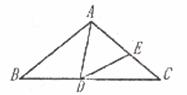
① 在图 2 中依题意补全图形，并求 ∠ ADB 的度数；

② 若 ∠ BCD 的平分线 CE 交 BD 于点 F ，交 DA 的延长线于点 E ，连结 BE ．用等式表示线段 AD 、 CE 、 BE 之间的数量关系，并证明．

答案

(1)135°

(2) （ 2 ） ① 补全图形见解析； ∠ ADB =45° ； ②2 BE - AD = CE ．理由见解析

【分析】（ 1 ）由题意得点 A 、 D 、 B 都在以 C 为圆心， CA 为半径的 ⊙ C 上，利用圆内接四边形的性质即可求解；

（ 2 ） ① 根据题意补全图形即可；同（ 1 ），利用圆周角定理即可求解；

② 过点 C 作 CH ⊥ EC 于点 C ，交 ED 的延长线于点 H ，证明 BE = DE ， △ CEH 是等腰直角三角形，推出 EH =2 BE - AD ，利用等腰直角三角形的性质即可证明结论．

【详解】（ 1 ）解：由题意得： CA = CD = CB ，

∴ 点 A 、 D 、 B 都在以 C 为圆心， CA 为半径的 ⊙ C 上，如图，

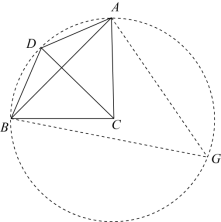
在优弧 上取点 G ，连接 AG ， BG ，

∵ Rt △ ABC 中， ∠ BCA =90° ，

∴∠ BGA =45° ，

∵ 四边形 ADBG 是圆内接四边形，

∴∠ ADB =180°-45°=135° ，

故答案为： 135° ；

（ 2 ） ① 补全图形，如图：

由题意得： CA = CD = CB ，

∴ 点 A 、 D 、 B 都在以 C 为圆心， CA 为半径的 ⊙ C 上，如图，

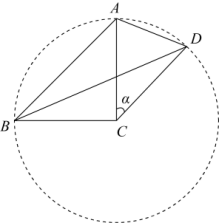
∵ Rt △ ABC 中， ∠ BCA =90° ，

∴∠ ADB =45° ；

②2 BE - AD = CE ．理由如下：

过点 C 作 CH ⊥ EC 于点 C ，交 ED 的延长线于点 H ，如图：

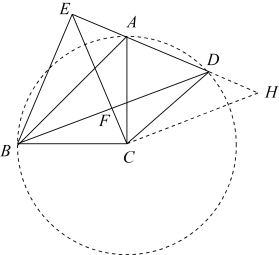
∵ CD = CB ， CE 是 ∠ BCD 的平分线，

∴ CE 是线段 BD 的垂直平分线，

∴ BE = DE ， ∠ EFD =90° ，

由 ① 知 ∠ ADB =45° ，

∴∠ DEF =45° ，

∴△ CEH 是等腰直角三角形，

∴∠ DEF =∠ H =45° ， CE = CH ，

∵ CD = CA ，

∴∠ CAD =∠ CDA ，则 ∠ CAE =∠ CDH ，

∴△ AEC ≌△ DHC ，

∴ AE = DH ，

∴ EH =2 ED - AD =2 BE - AD ，

∵△ CEH 是等腰直角三角形，

∴2 BE - AD = CE ．

【点睛】本题属于几何变换综合题，考查了旋转变换，全等三角形的判定和性质，圆内接四边形的性质，等腰直角三角形的判定和性质等知识，解题的关键是正确寻找全等三角形和等腰直角三角形解决问题．