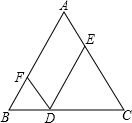
如图 , 在 中,
,
是
上的点 ,
∥
交
于点
,
∥
交
于点
,那么四边形
的周长是( )
A . 5 B . 10 C . 15 D . 20
答案
B
【分析】由于 DE ∥ AB , DF ∥ AC ,则可以推出四边形 AFDE 是平行四边形,然后利用平行四边形的性质可以证明 □ AFDE 的周长等于 AB + A C .
【详解】 ∵ DE ∥ AB , DF ∥ AC ,
则四边形 AFDE 是平行四边形,
∠ B = ∠ EDC , ∠ FDB = ∠ C
∵ AB = AC ,
∴∠ B = ∠ C ,
∴∠ B = ∠ FDB , ∠ C = ∠EDF ,
∴ BF = FD , DE = EC ,
所以 □ AFDE 的周长等于 AB + AC = 10 .
故答案为 B
【点睛】本题考查了平行四边形的性质、等腰三角形的性质、平行四边形的判定 , 熟练掌握这些知识点是本题解题的关键.