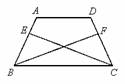
综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图 1 ,在正方形 ABCD 中, E 是 BC 的中点, , EP 与正方形的外角
的平分线交于 P 点.试猜想 AE 与 EP 的数量关系,并加以证明;
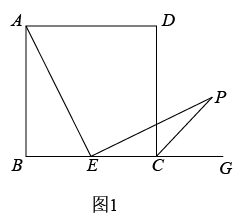
(1) 【思考尝试】同学们发现,取 AB 的中点 F ,连接 EF 可以解决这个问题.请在图 1 中补全图形,解答老师提出的问题.
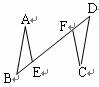
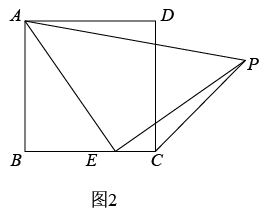
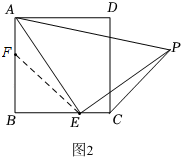
(2) 【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图 2 ,在正方形 ABCD 中, E 为 BC 边上一动点(点 E , B 不重合), 是等腰直角三角形,
,连接 CP ,可以求出
的大小,请你思考并解答这个问题.
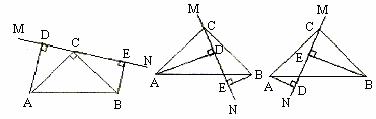
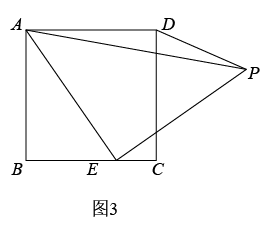
(3) 【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图 3 ,在正方形 ABCD 中, E 为 BC 边上一动点(点 E , B 不重合), 是等腰直角三角形,
,连接 DP .知道正方形的边长时,可以求出
周长的最小值.当
时,请你求出
周长的最小值.
答案
(1) 答案见解析
(2) ,理由见解析
(3) ,理由见解析
【分析】( 1 )取 AB 的中点 F ,连接 EF ,利用同角的余角相等说明 ∠ PEC = ∠ BAE ,再根据 ASA 证明 △ AFE ≌△ ECP ,得 AE = EP ;
( 2 )在 AB 上取 AF = EC ,连接 EF ,由( 1 )同理可得 ∠ CEP = ∠ FAE ,则 △ FAE ≌△ CEP ( SAS ),再说明 △ BEF 是等腰直角三角形即可得出答案;
( 3 )作 DG ⊥ CP ,交 BC 的延长线于 G ,交 CP 于 O ,连接 AG ,则 △ DCG 是等腰直角三角形,可知点 D 与 G 关于 CP 对称,则 AP + DP 的最小值为 AG 的长,利用勾股定理求出 AG ,进而得出答案.
( 1 )
解: AE = EP ,
理由如下:取 AB 的中点 F ,连接 EF ,
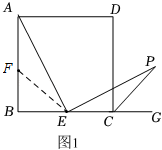
∵ F 、 E 分别为 AB 、 BC 的中点,
∴ AF = BF = BE = CE ,
∴∠ BFE = 45° ,
∴∠ AFE = 135° ,
∵ CP 平分 ∠ DCG ,
∴∠ DCP = 45° ,
∴∠ ECP = 135° ,
∴∠ AFE = ∠ ECP ,
∵ AE ⊥ PE ,
∴∠ AEP = 90° ,
∴∠ AEB +∠ PEC = 90° ,
∵∠ AEB +∠ BAE = 90° ,
∴∠ PEC = ∠ BAE ,
∴△ AFE ≌△ ECP ( ASA ),
∴ AE = EP ;
( 2 )
解:在 AB 上取 AF = EC ,连接 EF ,
由( 1 )同理可得 ∠ CEP = ∠ FAE ,
∵ AF = EC , AE = EP ,
∴△ FAE ≌△ CEP ( SAS ),
∴∠ ECP = ∠ AFE ,
∵ AF = EC , AB = BC ,
∴ BF = BE ,
∴∠ BEF = ∠ BFE = 45° ,
∴∠ AFE = 135° ,
∴∠ ECP = 135° ,
∴∠ DCP = 45° ;
( 3 )
解:作 DG ⊥ CP ,交 BC 的延长线于 G ,交 CP 于 O ,连接 AG ,
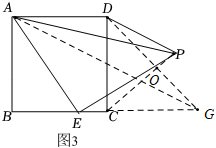
由( 2 )知, ∠ DCP = 45° ,
∴∠ CDG = 45° ,
∴△ DCG 是等腰直角三角形,
∴ 点 D 与 G 关于 CP 对称,
∴ AP + DP 的最小值为 AG 的长,
∵ AB = 4 ,
∴ BG = 8 ,
由勾股定理得 AG = ,
∴△ ADP 周长的最小值为 AD + AG = .
【点睛】本题是四边形综合题,主要考查了正方形的性质,轴对称﹣最短路线问题,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,作辅助线构造全等三角形是解题的关键.