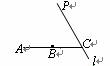
如图， 内接于 ， CD 是 的直径， ，则 （ ）

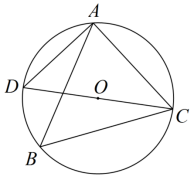
A ． 70° B ． 60° C ． 50° D ． 40°

答案

C

【分析】由 CD 是 ⊙ O 的直径，根据直径所对的圆周角是直角，得出 ∠ CAD ＝ 90° ，根据直角三角形两锐角互余得到 ∠ ACD 与 ∠ D 互余，即可求得 ∠ D 的度数，继而求得 ∠ B 的度数．

【详解】解： ∵ CD 是 ⊙ O 的直径，

∴∠ CAD ＝ 90° ，

∴∠ ACD +∠ D ＝ 90° ，

∵∠ ACD ＝ 40° ，

∴∠ ADC ＝ ∠ B ＝ 50° ．

故选： C ．

【点睛】本题考查了圆周角定理，直角三角形的性质，注意掌握数形结合思想是解题的关键．